Abstracting Code Patterns

a.k.a. Dont Repeat Yourself

Lists

data List a
  = []
  | (:) a (List a)

Rendering the Values of a List

-- >>> incList [1, 2, 3]
-- ["1", "2", "3"]

showList        :: [Int] -> [String]
showList []     =  []
showList (n:ns) =  show n : showList ns

Squaring the values of a list

-- >>> sqrList [1, 2, 3]
-- 1, 4, 9

sqrList        :: [Int] -> [Int]
sqrList []     =  []
sqrList (n:ns) =  n^2 : sqrList ns

Common Pattern: map over a list

Refactor iteration into mapList

mapList :: (a -> b) -> [a] -> [b]
mapList f []     = []
mapList f (x:xs) = f x : mapList f xs

Reuse map to implement inc and sqr

showList xs = map (\n -> show n) xs

sqrList  xs = map (\n -> n ^ 2)  xs

Trees

data Tree a
  = Leaf
  | Node a (Tree a) (Tree a)

Incrementing and Squaring the Values of a Tree

-- >>> showTree (Node 2 (Node 1 Leaf Leaf) (Node 3 Leaf Leaf))
-- (Node "2" (Node "1" Leaf Leaf) (Node "3" Leaf Leaf))

showTree :: Tree Int -> Tree String
showTree Leaf         = ???
showTree (Node v l r) = ???

-- >>> sqrTree (Node 2 (Node 1 Leaf Leaf) (Node 3 Leaf Leaf))
-- (Node 4 (Node 1 Leaf Leaf) (Node 9 Leaf Leaf))

sqrTree :: Tree Int -> Tree Int
sqrTree Leaf         = ???
sqrTree (Node v l r) = ???

QUIZ: map over a Tree

Refactor iteration into mapTree! What should the type of mapTree be?

mapTree :: ???

showTree t = mapTree (\n -> show n) t
sqrTree  t = mapTree (\n -> n ^ 2)  t

{- A -} (Int -> Int)    -> Tree Int -> Tree Int
{- B -} (Int -> String) -> Tree Int -> Tree String
{- C -} (Int -> a)      -> Tree Int -> Tree a
{- D -} (a -> a)        -> Tree a   -> Tree a
{- E -} (a -> b)        -> Tree a   -> Tree b

Lets write mapTree

mapTree :: (a -> b) -> Tree a -> Tree b
mapTree f Leaf         = ???
mapTree f (Node v l r) = ???

QUIZ

Wait … there is a common pattern across two datatypes

type List a = [a]
mapList :: (a -> b) -> List a -> List b    -- List
mapTree :: (a -> b) -> Tree a -> Tree b    -- Tree

gmap    :: (Mappable t) => (a -> b) -> t a  -> t b

Lets make a class for it!

class Functor t where
  fmap :: ???

What type should we give to fmap?

{- A -} (b -> a) -> t b    -> t a
{- B -} (a -> a) -> t a    -> t a
{- C -} (a -> b) -> [a]    -> [b]
{- D -} (a -> b) -> t a    -> t b
{- E -} (a -> b) -> Tree a -> Tree b

Reuse Iteration Across Types

instance Functor [] where
  fmap = mapList

instance Functor Tree where
  fmap = mapTree

And now we can do

-- >>> fmap (\n -> n + 1) (Node 2 (Node 1 Leaf Leaf) (Node 3 Leaf Leaf))
-- (Node 4 (Node 1 Leaf Leaf) (Node 9 Leaf Leaf))

-- >>> fmap show [1,2,3]
-- ["1", "2", "3"]

Exercise: Write a Functor instance for Result

data Result  a
  = Error String
  | Ok    a

instance Functor Result where
  fmap f (Error msg) = ???
  fmap f (Ok val)    = ???

When you’re done you should see

-- >>> fmap (\n -> n ^ 2) (Error "oh no") Node 2 (Node 1 Leaf Leaf) (Node 3 Leaf Leaf))
-- (Node 4 (Node 1 Leaf Leaf) (Node 9 Leaf Leaf))

Next: A Class for Sequencing

Recall our old Expr datatype

data Expr
  = Number Int
  | Plus   Expr Expr
  | Div    Expr Expr
  deriving (Show)

eval :: Expr -> Int
eval (Number n)   = n
eval (Plus e1 e2) = eval e1   +   eval e2
eval (Div  e1 e2) = eval e1 `div` eval e2

-- >>> eval (Div (Number 6) (Number 2))
-- 3

But, what is the result

-- >>> eval (Div (Number 6) (Number 0))
-- *** Exception: divide by zero

A crash! Lets look at an alternative approach to avoid dividing by zero.

The idea is to return a Result Int (instead of a plain Int)

• If a sub-expression had a divide by zero, return Error "..."
• If all sub-expressions were safe, then return the actual Result v

eval :: Expr -> Result Int
eval (Number n)   = Value n
eval (Plus e1 e2) = case e1 of
                      Error err1 -> Error err1
                      Value v1   -> case e2 of
                                      Error err2 -> Error err2
                                      Value v1   -> Result (v1 + v2)
eval (Div e1 e2)  = case e1 of
                      Error err1 -> Error err1
                      Value v1   -> case e2 of
                                      Error err2 -> Error err2
                                      Value v1   -> if v2 == 0 
                                                      then Error ("yikes dbz:" ++ show e2)
                                                      else Value (v1 `div` v2)

The good news, no nasty exceptions, just a plain Error result

λ> eval (Div (Number 6) (Number 2))
Value 3
λ> eval (Div (Number 6) (Number 0))
Error "yikes dbz:Number 0"
λ> eval (Div (Number 6) (Plus (Number 2) (Number (-2))))
Error "yikes dbz:Plus (Number 2) (Number (-2))"

The bad news: the code is super duper gross

Lets spot a Pattern

The code is gross because we have these cascading blocks

case e1 of
  Error err1 -> Error err1
  Value v1   -> case e2 of
                  Error err2 -> Error err2
                  Value v1   -> Result (v1 + v2)

but really both blocks have something common pattern

case e of
  Error err -> Error err
  Value v   -> {- do stuff with v -}

1. Evaluate e
2. If the result is an Error then return that error.
3. If the result is a Value v then do some further processing on v.

Lets bottle that common structure in two functions:

• >>= (pronounced bind)
• return (pronounced return)

(>>=) :: Result a -> (a -> Result b) -> Result b
(Error err) >>= _       = Error err
(Value v)   >>= process = process v

return :: a -> Result a
return v = Value v

NOTE: return is not a keyword; it is just the name of a function!

A Cleaned up Evaluator

The magic bottle lets us clean up our eval

eval :: Expr -> Result Int
eval (Number n)   = return n
eval (Plus e1 e2) = eval e1 >>= \v1 ->
                    eval e2 >>= \v2 ->
                    return (v1 + v2)
eval (Div e1 e2)  = eval e1 >>= \v1 ->
                    eval e2 >>= \v2 ->
                    if v2 == 0
                      then Error ("yikes dbz:" ++ show e2)
                      else return (v1 `div` v2)

The gross pattern matching is all hidden inside >>=

Notice the >>= takes two inputs of type:

• Result Int (e.g. eval e1 or eval e2)
• Int -> Result Int (e.g. The processing function that takes the v and does stuff with it)

In the above, the processing functions are written using \v1 -> ... and \v2 -> ...

NOTE: It is crucial that you understand what the code above is doing, and why it is actually just a “shorter” version of the (gross) nested-case-of eval.

A Class for >>=

Like fmap or show or jval or ==, the >>= operator is useful across many types, so we capture it in an interface/typeclass:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

Notice how the definitions for Result fit the above, with m = Result

instance Monad Result where
  (>>=) :: Either a -> (a -> Either b) -> Either b
  (Error err) >>= _       = Error err
  (Value v)   >>= process = process v

  return :: a -> Result a
  return v = Value v

Syntax for >>=

In fact >>= is so useful there is special syntax for it.

Instead of writing

e1 >>= \v1 ->
e2 >>= \v2 ->
e3 >>= \v3 ->
e

you can write

do v1 <- e1
   v2 <- e2
   v3 <- e3
   e
...

Thus, we can further simplify our eval to:

eval :: Expr -> Result Int
eval (Number n)   = return n
eval (Plus e1 e2) = do v1 <- eval e1
                       v2 <- eval e2
                       return (v1 + v2)
eval (Div e1 e2)  = do v1 <- eval e1
                       v2 <- eval e2
                       if v2 == 0
                         then Error ("yikes dbz:" ++ show e2)
                         else return (v1 `div` v2)

Writing Applications

In most language related classes, we start with a “Hello world!” program.

With 130, we will end with it.

Purity and the Immutability Principle

Haskell is a pure language. Not a value judgment, but a precise technical statement:

The “Immutability Principle”:

• A function must always return the same output for a given input

• A function’s behavior should never change

No Side Effects

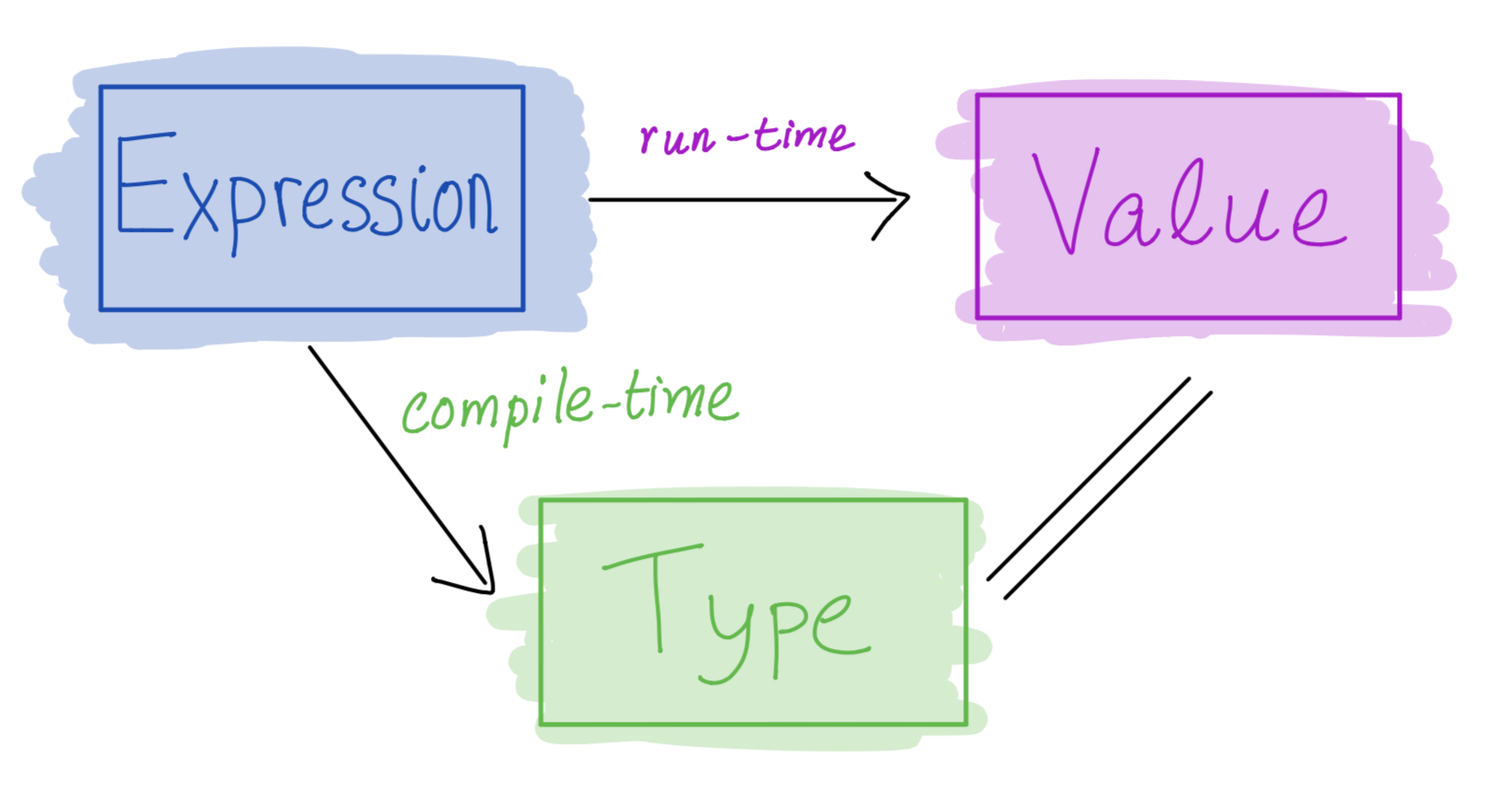
Haskell’s most radical idea: expression ==> value

• When you evaluate an expression you get a value and nothing else happens

Specifically, evaluation must not have an side effects

• change a global variable or

• print to screen or

• read a file or

• send an email or

• launch a missile.

Purity

Means functions may depend only on their inputs

• i.e. functions should give the same output for the same input every time.

But… how to write “Hello, world!”

But, we want to …

• print to screen
• read a file
• send an email

A language that only lets you write factorial and fibonacci is … not very useful!

Thankfully, you can do all the above via a very clever idea: Recipe

Recipes

This analogy is due to Joachim Brietner

Haskell has a special type called IO – which you can think of as Recipe

type Recipe a = IO a

A value of type Recipe a is

• a description of an effectful computations

• when when executed (possibly) perform some effectful I/O operations to

• produce a value of type a.

Recipes have No Effects

A value of type Recipe a is

• Just a description of an effectful computation

• An inert, perfectly safe thing with no effects.

(L) chocolate cake, (R) a sequence of instructions on how to make a cake.

They are different (hint: only one of them is delicious.)

Merely having a Recipe Cake has no effects: holding the recipe

• Does not make your oven hot

• Does not make your your floor dirty

Executing Recipes

There is only one way to execute a Recipe a

Haskell looks for a special value

main :: Recipe ()

The value associated with main is handed to the runtime system and executed

The Haskell runtime is a master chef who is the only one allowed to cook!

How to write an App in Haskell

Make a Recipe () that is handed off to the master chef main.

• main can be arbitrarily complicated

• will be composed of many smaller recipes

Hello World

putStrLn :: String -> Recipe ()

The function putStrLn

• takes as input a String
• returns as output a Recipe ()

putStrLn msg is a Recipe () when executed prints out msg on the screen.

main :: Recipe ()
main = putStrLn "Hello, world!"

… and we can compile and run it

$ ghc --make hello.hs
$ ./hello
Hello, world!

QUIZ: Combining Recipes

Next, lets write a program that prints multiple things:

main :: IO ()
main = combine (putStrLn "Hello,") (putStrLn "World!")

-- putStrLn :: String -> Recipe ()
-- combine  :: ???

What must the type of combine be?

{- A -} combine :: () -> () -> ()
{- B -} combine :: Recipe () -> Recipe () -> Recipe ()
{- C -} combine :: Recipe a  -> Recipe a  -> Recipe a
{- D -} combine :: Recipe a  -> Recipe b  -> Recipe b
{- E -} combine :: Recipe a  -> Recipe b  -> Recipe a

Using Intermediate Results

Next, lets write a program that

1. Asks for the user’s name using

    getLine :: Recipe String

2. Prints out a greeting with that name using

    putStrLn :: String -> Recipe ()

Problem: How to pass the output of first recipe into the second recipe?

QUIZ: Using Yolks to Make Batter

Suppose you have two recipes

crack     :: Recipe Yolk
eggBatter :: Yolk -> Recipe Batter

and we want to get

mkBatter :: Recipe Batter
mkBatter = crack `combineWithResult` eggBatter

What must the type of combineWithResult be?

{- A -} Yolk -> Batter -> Batter
{- B -} Recipe Yolk -> (Yolk  -> Recipe Batter) -> Recipe Batter
{- C -} Recipe a    -> (a     -> Recipe a     ) -> Recipe a
{- D -} Recipe a    -> (a     -> Recipe b     ) -> Recipe b
{- E -} Recipe Yolk -> (Yolk  -> Recipe Batter) -> Recipe ()

Looks Familar

Wait a bit, the signature looks familiar!

combineWithResult :: Recipe a -> (a -> Recipe b) -> Recipe b

Remember this

(>>=)             :: Result a -> (a -> Result b) -> Result b

Recipe is an instance of Monad

In fact, in the standard library

instance Monad Recipe where
  (>>=) = {-... combineWithResult... -}

So we can put this together with putStrLn to get:

main :: Recipe ()
main = getLine >>= \name -> putStrLn ("Hello, " ++ name ++ "!")

or, using do notation the above becomes

main :: Recipe ()
main = do name <- getLine
          putStrLn ("Hello, " ++ name ++ "!")

Exercise

1. Compile and run to make sure its ok!
2. Modify the above to repeatedly ask for names.
3. Extend the above to print a “prompt” that tells you how many iterations have occurred.

Monads are Amazing

Monads have had a revolutionary influence in PL, well beyond Haskell, some recent examples

• Error handling in go e.g. 1 and 2

• Asynchrony in JavaScript e.g. 1 and 2

• Big data pipelines e.g. LinQ and TensorFlow

A Silly App to End CSE 130

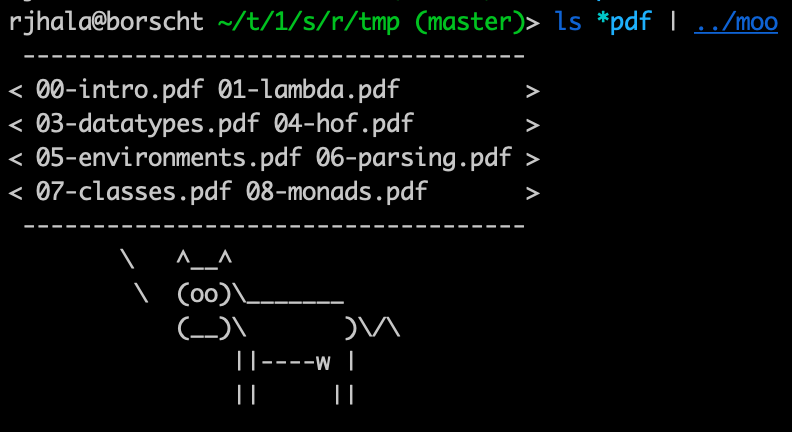
Lets write an app called moo inspired by cowsay

A Command Line App

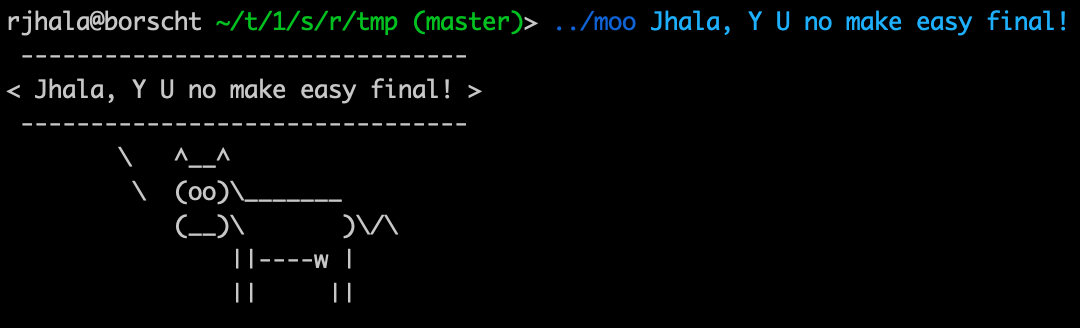
moo works with pipes