Functions and Programming

What is Haskell?

A typed, lazy, purely functional programming language

Haskell = λ-calculus ++

• better syntax
• types
• built-in features
  • booleans, numbers, characters
  • records (tuples)
  • lists
  • recursion
  • …

Why Haskell?

Haskell programs tend to be simple and correct

QuickSort in Haskell

sort        :: (Ord a) => [a] -> [a]
sort []     = []
sort (x:xs) = sort ls ++ [x] ++ sort rs
  where
    ls      = [ l | l <- xs, l <= x ]
    rs      = [ r | r <- xs, x <  r ]

Goals for this week

1. Understand the code above
2. Understand what typed, lazy, and purely functional means (and why it’s cool)

Haskell vs λ-calculus: similarities

(1) Programs

A program is an expression (not a sequence of statements)

It evaluates to a value (it does not perform actions)

• λ:

  (\x -> x) apple     -- =~> apple

• Haskell:

  (\x -> x) "apple"   -- =~> "apple"

(2) Functions

Functions are first-class values:

• can be passed as arguments to other functions
• can be returned as results from other functions
• can be partially applied (arguments passed one at a time)

(\x -> (\y -> x (x y))) (\z -> z + 1) 0   -- =~> ???

But: unlike λ-calculus, not everything is a function!

(3) Top-level bindings

Like in Elsa, we can name terms to use them later

Elsa:

let T    = \x y -> x
let F    = \x y -> y

let PAIR = \x y -> \b -> ITE b x y
let FST  = \p -> p T
let SND  = \p -> p F

eval fst:
 FST (PAIR apple orange)
 =~> apple

Haskell:

haskellIsAwesome = True

pair = \x y -> \b -> if b then x else y
fst = \p -> p haskellIsAwesome
snd = \p -> p False

-- In GHCi:
> fst (pair "apple" "orange")   -- "apple"

The names are called top-level variables

Their definitions are called top-level bindings

Better Syntax: Equations and Patterns

You can define function bindings using equations:

pair x y b = if b then x else y -- same as: pair = \x y b -> ...
fst p      = p True             -- same as: fst = \p -> ...
snd p      = p False            -- same as: snd = \p -> ...

A single function binding can have multiple equations with different patterns of parameters:

pair x y True  = x  -- If 3rd arg matches True,
                    -- use this equation;
pair x y False = y  -- Otherwise, if 3rd arg matches False,
                    -- use this equation.

At run time, the first equation whose pattern matches the actual arguments is chosen

For now, a pattern is:

• a variable (matches any value)

• or a value (matches only that value)

Same as:

pair x y True  = x  -- If 3rd arg matches True,
                    -- use this equation;
pair x y b     = y  -- Otherwise, use this equation.

Same as:

pair x y True  = x
pair x y _     = y

QUIZ

Which of the following definitions of pair is incorrect?

A. pair x y = \b -> if b then x else y

B. pair x = \y b -> if b then x else y

C.

pair x _ True  = x
pair _ y _     = y

D.

pair x y b     = x
pair x y False = y

E. all of the above

Equations with guards

An equation can have multiple guards (Boolean expressions):

cmpSquare x y  |  x > y*y   =  "bigger :)"
               |  x == y*y  =  "same :|"
               |  x < y*y   =  "smaller :("

Same as:

cmpSquare x y  |  x > y*y   =  "bigger :)"
               |  x == y*y  =  "same :|"
               |  otherwise =  "smaller :("

Recusion

Recursion is built-in, so you can write:

sum n = if n == 0 
          then 0 
          else n + sum (n - 1)

or you can write:

sum 0 = 0
sum n = n + sum (n - 1)

The scope of variables

Top-level variable have global scope, so you can write:

message = if haskellIsAwesome          -- this var defined below
            then "I love CSE 130"
            else "I'm dropping CSE 130"
            
haskellIsAwesome = True

Or you can write:

-- What does f compute?
f 0 = True
f n = g (n - 1) -- mutual recursion!

g 0 = False
g n = f (n - 1) -- mutual recursion!

Is this allowed?

haskellIsAwesome = True

haskellIsAwesome = False -- changed my mind

Local variables

You can introduce a new (local) scope using a let-expression:

sum 0 = 0
sum n = let n' = n - 1          
        in n + sum n'  -- the scope of n' is the term after in

Syntactic sugar for nested let-expressions:

sum 0 = 0
sum n = let 
          n'   = n - 1
          sum' = sum n'
        in n + sum'

If you need a variable whose scope is an equation, use the where clause instead:

cmpSquare x y  |  x > z   =  "bigger :)"
               |  x == z  =  "same :|"
               |  x < z   =  "smaller :("
  where z = y*y

Types

What would Elsa say?

let WEIRDO = ONE ZERO

What would Python say?

def weirdo():
  return 0(1)

What would Java say?

void weirdo() {
  int zero;
  zero(1);
}

Types

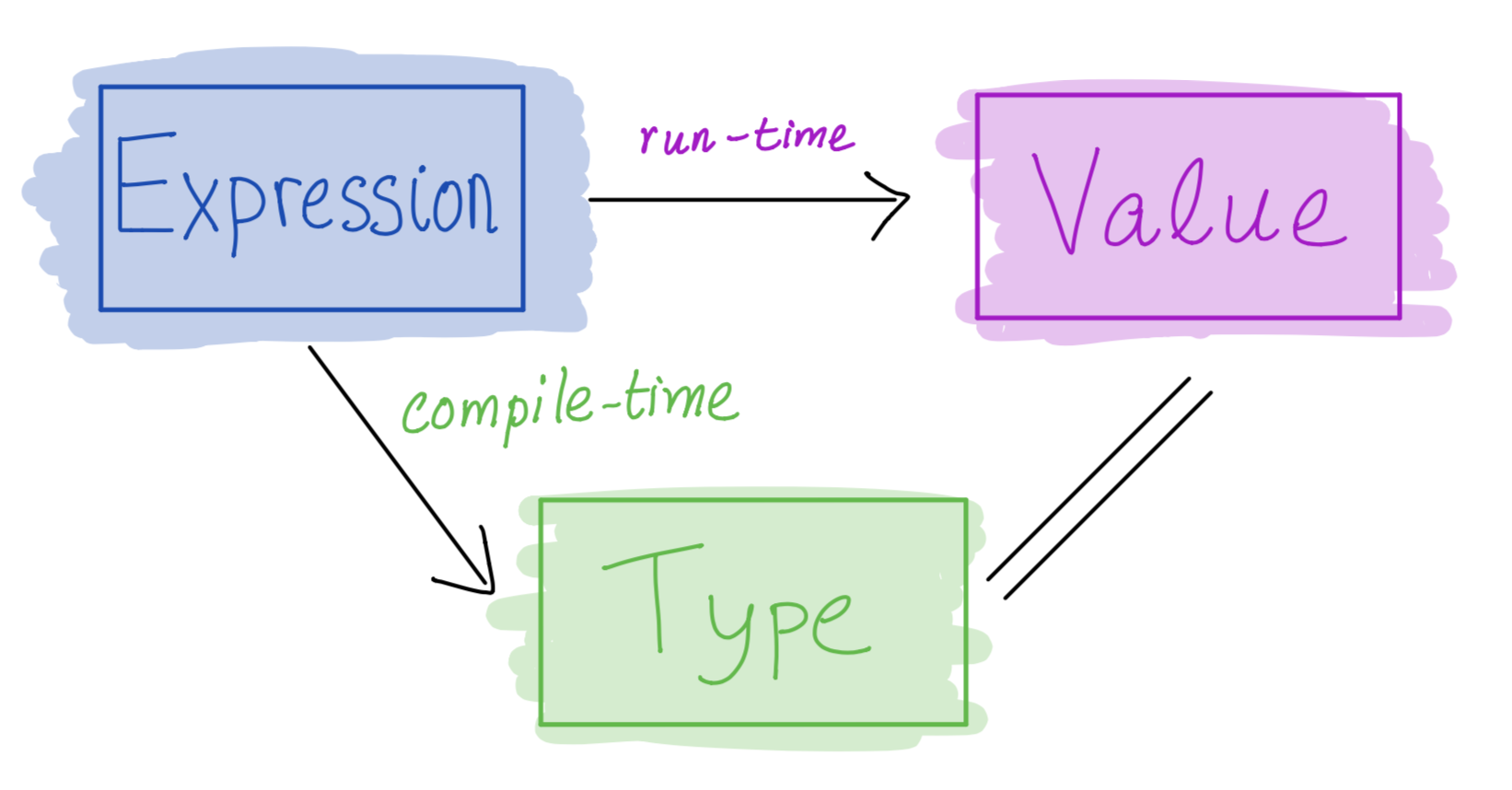
In Haskell every expression either

• ill-typed and rejected at compile time or
• has a type and can be evaluated to obtain _ a value of the same type.

Ill-typed* expressions are rejected statically at compile-time, before execution starts

• like in Java
• unlike λ-calculus or Python …

weirdo = 1 0     -- rejected by GHC

Why are types good?

• Helps with program design
• Types are contracts (ignore ill-typed inputs!)
• Catches errors early
• Allows compiler to generate code
• Enables compiler optimizations

Type annotations

You can annotate your bindings with their types using ::, like so:

-- | This is a Boolean:
haskellIsAwesome :: Bool            
haskellIsAwesome = True

-- | This is a string
message :: String
message = if haskellIsAwesome
            then "I love CSE 130"
            else "I'm dropping CSE 130"
            
-- | This is a word-size integer
rating :: Int
rating = if haskellIsAwesome then 10 else 0

-- | This is an arbitrary precision integer
bigNumber :: Integer
bigNumber = factorial 100

If you omit annotations, GHC will infer them for you

• Inspect types in GHCi using :t
• You should annotate all top-level bindings anyway! (Why?)

Function Types

Functions have arrow types:

• \x -> e has type A -> B
• if e has type B assuming x has type A

For example:

> :t (\x -> if x then `a` else `b`)  -- ???

Always annotate your function bindings

First understand what the function does

• Before you think about how to do it

sum :: Int -> Int
sum 0 = 0
sum n = n + sum (n - 1)

When you have *multiple arguments

For example

add3 :: Int -> (Int -> (Int -> Int))
add3 x y z = x + y + z

why? because the above is the same as:

add3 :: Int -> (Int -> (Int -> Int))
add3 = \x -> (\y -> (\z -> x + y + z))

however, as with the lambdas, the -> associates to the right so we will just write:

add3 :: Int -> Int -> Int -> Int
add3 x y z = x + y + z

Lists

A list is

• either an empty list

  [] -- pronounced "nil"

• or a head element attached to a tail list

  h : t -- pronounced "h cons t"

Examples:

[]                -- A list with zero elements

1 : []            -- A list with one element: 1

(:) 1 []          -- As above: for any infix op, `x op y` is same as `(op) x y`

1:(2:(3:(4:[])))  -- A list with four elements: 1, 2, 3, 4

1:2:3:4:[]        -- Same thing (: is right associative)

[1,2,3,4]         -- Same thing (syntactic sugar)

Terminology: constructors and values

[] and (:) are called the list constructors

We’ve seen constructors before:

• True and False are Bool constructors
• 0, 1, 2 are … well, you can think of them as Int constructors
  • The Int constructors don’t take any parameters, we just called them values

In general, a value is a constructor applied to other values

• examples above are list values

The Type of a List

A list has type [Thing] if each of its elements has type Thing

Examples:

intList :: [Int]
intList = [1,2,3,4]

boolList :: [Bool]
boolList = [True, False, True]

strList :: [String]
strList = ["nom", "nom", "burp"]

Lets write some Functions

A Recipe

Step 1: Write some tests

Step 2: Write the type

Step 3: Write the code

Functions on lists: range

1. Tests

-- >>> ???

2. Type

range :: ???

3. Code

range = ???

Syntactic Sugar for Ranges

There’s also syntactic sugar for this!

[1..7]    -- [1,2,3,4,5,6,7]
[1,3..7]  -- [1,3,5,7]

Functions on lists: length

1. Tests

-- >>> ???

2. Type

len :: ???

3. Code

len = ???

Pattern matching on lists

-- | Length of the list
len :: [Int] -> Int
len []     = 0
len (_:xs) = 1 + len xs

A pattern is either a variable (incl. _) or a value

A pattern is

• either a variable (incl. _)
• or a constructor applied to other patterns

Pattern matching attempts to match values against patterns and, if desired, bind variables to successful matches.

Functions on lists: take

Let’s write a function to take first n elements of a list xs.

1. Tests

-- >>> ???

2. Type

take :: ???

3. Code

take = ???

QUIZ

Which of the following is not a pattern?

A. (1:xs)

B. (_:_:_)

C. [x]

D. [1+2,x,y]

E. all of the above

Strings are Lists-of-Chars

For example

λ> let x = ['h', 'e', 'l', 'l', 'o']
λ> x
"hello"

λ> let y = "hello"

λ> x == y
True

λ> :t x
x :: [Char]

λ> :t y
y :: [Char]

shout Shout SHOUT

How can we convert a string to upper-case, e.g.

ghci> shout "like this"
"LIKE THIS"

shout :: String -> String
shout s = ???

Some useful library functions

-- | Length of the list
length :: [t] -> Int

-- | Append two lists
(++) :: [t] -> [t] -> [t]

-- | Are two lists equal?
(==) :: [t] -> [t] -> Bool

You can search for library functions on Hoogle!

Tuples

myPair :: (String, Int)  -- pair of String and Int
myPair = ("apple", 3)

(,) is the pair constructor

Field access

Using fst and snd

ghci> fst ("apple", 22)
"apple"

ghci> snd ("apple", 22)
22

Tuples to pass parameters

add2 :: (Int, Int) -> Int
add2 p = fst p + snd p

but watch out, add2 expects a tuple.

exAdd2_BAD = add2 10 20      -- type error

exAdd2_OK  = add2 (10, 20)   -- OK!

Tuples and Pattern Matching

It is often clearer to use patterns for tuples, e.g.

add2 :: (Int, Int) -> Int
add2 p = let (x, y) = p in
           x + y

or equivalently,

add2 :: (Int, Int) -> Int
add2 p    = x + y
  where
   (x, y) = p

or, best, use the pattern in the parameter,

add2 :: (Int, Int) -> Int
add2 (x, y) = x + y

You can use pattern matching not only in equations, but also in λ-bindings and let-bindings!

QUIZ: Pattern matching with pairs

Is this pattern matching correct? What does this function do?

quiz :: String -> [(String, Int)] -> Int
quiz _ []     = 0
quiz x ((k,v) : ps)
  | x == k    = v
  | otherwise = quiz x ps

What is quiz "dog" [ ("cat", 10), ("dog", 20), ("cat", 30)] ?

A. Type error!

B. 0

C. 10

D. 20

D. 30

Generalized Tuples

Can we implement triples like in λ-calculus?

Sure! but Haskell has native support for n-tuples:

myPair   :: (String, Int)
myPair   = ("apple", 3)

myTriple :: (Bool, Int, [Int])
myTriple = (True, 1, [1,2,3])

my4tuple :: (Float, Float, Float, Float)
my4tuple = (pi, sin pi, cos pi, sqrt 2)

The “Empty” Tuple

It also makes sense to have an 0-ary tuple:

myUnit :: ()
myUnit = ()

often used like void in other languages.

List comprehensions

A convenient way to construct lists!

QUIZ

What is the result of evaluating:

quiz = [ 10 * i | i <- [0,1,2,3,4,5]]

A. Infinite loop B. [] C. [0, 10, 20, 30, 40, 50] D. 150 E. Type error

Comprehensions and Ranges

Recall you can enumerate ranges as

ghci> [0..5]
[0,1,2,3,4,5]

So, we can write the above more simply

quiz = [ 10 * i | i <- [0..5] ]

QUIZ: Composing Comprehensions

What is the result of evaluating

quiz = [(i,j) | i <- [0, 1]     -- a first selection
              , j <- [0, 1] ]   -- a second selection

A. Type error B. [] C. [0,1] D. [(0,0), (1,1)] E. [(0,0), (0,1, (1,0), (1,1)]

QUIZ: Composing Comprehensions

What is the result of evaluating

quiz = [(i,j) | i <- [0, 1]
              , j <- [0, 1]
              , i == j      ]   -- condition!

A. Type error B. [] C. [0,1] D. [(0,0), (1,1)] E. [(0,0), (0,1, (1,0), (1,1)]

shout revisited

How can we convert a string to upper-case, e.g.

ghci> shout "like this"
"LIKE THIS"

Use comprehensions to write a *non-recursive" shout?

shout :: String -> String
shout s = ???

QuickSort in Haskell

Step 1: Write some tests

-- >>> sort []
-- ???

-- >>> sort [10]
-- ???

-- >>> sort [12, 1, 10]
-- ???

Step 2: Write the type

sort :: ???

Step 3: Write the code

sort []     = ???
sort (x:xs) = ???

sort :: [Int] -> [Int]
sort []     = []
sort (x:xs) = sort ls ++ [x] ++ sort rs
  where
    ls      = [ l | l <- xs, l <= x ]
    rs      = [ r | r <- xs, x <  r ]

Haskell is purely functional

Functional = functions are first-class values

Pure = a program is an expression that evaluates to a value

• no side effects!

• unlike in Python, Java, etc:

  public int f(int x) {
    calls++;                         // side effect: global variable update!
    System.out.println("calling f"); // side effect: writing to screen!
    launchMissile();                 // side effect: can't bring back home!
    return x * 2;
  }

• in Haskell, a function of type Int -> Int Computes a single integer output from a single integer input Does nothing else

Referential transparency: The same expression always evaluates to the same value

Why is this good?

• easier to reason about (remember x++ vs ++x in C++?)
• enables compiler optimizations
• especially great for parallelization (e1 + e2: we can always compute e1 and e2 in parallel!)

QUIZ

The function head returns the first element of a list.

What is the result of:

goBabyGo :: Int -> [Int]
goBabyGo n = n : goBabyGo (n + 1)

quiz :: Int
quiz = head (goBabyGo 0)

A. Loops forever B. Type error C. 0 D. 1

Haskell is Lazy

An expression is evaluated only when its result is needed!

ghci> take 2 (goBabyGo 1)
[1,2]

Why?

        take 2 (goBabyGo 1)
=>      take 2 (1 : goBabyGo 2)
=>      take 2 (1 : 2 : goBabyGo 3)
=> 1:   take 1 (    2 : goBabyGo 3)
=> 1:2: take 0 (        goBabyGo 3)
=> 1:2: []

Why is this good?

• can implement cool stuff like infinite lists: [1..]

  -- first n pairs of co-primes: 
  take n [(i,j) | i <- [1..],
                  j <- [1..i],
                  gcd i j == 1]

• encourages simple, general solutions

• but has its problems too :(

That’s all folks!