Past three weeks

How to use essential language constructs?

• Data Types
• Recursion
• Higher-Order Functions

Next two weeks

How to implement language constructs?

• Local variables and scope
• Environments and Closures
• (skip) Type Inference

Interpreter

How do we represent and evaluate a program?

Roadmap: The Nano Language

Features of Nano:

1. Arithmetic
2. Variables
3. Let-bindings
4. Functions
5. Recursion

1. Nano: Arithmetic

A “grammar” of arithmetic expressions:

e ::= n
    | e1 + e2
    | e1 - e2
    | e1 * e2

Representing Arithmetic Expressions and Values

Lets represent arithmetic expressions as type

data Expr
  = ENum Int         -- ^ n
  | EAdd Expr Expr   -- ^ e1 + e2
  | ESub Expr Expr   -- ^ e1 - e2
  | EMul Expr Expr   -- ^ e1 * e2

Lets represent arithmetic values as a type

type Value = Int

Evaluating Arithmetic Expressions

We can now write a Haskell function to evaluate an expression:

eval :: Expr -> Value
eval (ENum n)     = n
eval (EAdd e1 e2) = eval e1 + eval e2
eval (ESub e1 e2) = eval e1 - eval e2
eval (EMul e1 e2) = eval e1 * eval e2

Alternative representation

Lets pull the operators into a separate type

data Binop = Add                  -- ^ `+`
           | Sub                  -- ^ `-`
           | Mul                  -- ^ `*`

data Expr  = ENum Int              -- ^ n
           | EBin Binop Expr Expr  -- ^ e1 `op` e2

QUIZ

Evaluator for alternative representation

eval :: Expr -> Value
eval (ENum n)        = n
eval (EBin op e1 e2) = evalOp op (eval e1) (eval e2)

What is a suitable type for evalOp?

{- 1 -} evalOp :: BinOp -> Value
{- 2 -} evalOp :: BinOp -> Value -> Value -> Value
{- 3 -} evalOp :: BinOp -> Expr  -> Expr -> Value
{- 4 -} evalOp :: BinOp -> Expr -> Expr -> Expr
{- 5 -} evalOp :: BinOp -> Expr -> Value

The Nano Language

Features of Nano:

1. Arithmetic [done]
2. Variables
3. Let-bindings
4. Functions
5. Recursion

2. Nano: Variables

Let’s add variables and let bindings!

e ::= n                   -- OLD
    | e1 + e2
    | e1 - e2
    | e1 * e2
                          -- NEW
    | x                   -- variables

Lets extend our datatype

type Id = String

data Expr
  = ENum Int              -- OLD
  | EBin Binop Expr Expr  
                         -- NEW
  | EVar Id              -- variables

QUIZ

What should the following expression evaluate to?

x + 1

(A) 0

(B) 1

(C) Error

Environment

An expression is evaluated in an environment

• A phone book which maps variables to values

[ "x" := 0, "y" := 12, ...]

A type for environments

type Env = [(Id, Value)]

Evaluation in an Environment

We write

(eval env expr) ==> value

to mean

When expr is evaluated in environment env the result is value

That is, when we have variables, we modify our evaluator to take an input environment env in which expr must be evaluated.

eval :: Env -> Expr -> Value
eval env expr = ... value-of-expr-in-env...

First, lets update the evaluator for the arithmetic cases ENum and EBin

eval :: Env -> Expr -> Value
eval env (ENum n)        = ???
eval env (EBin op e1 e2) = ???

QUIZ

What is a suitable ?value such that

eval [ "x" := 0, "y" := 12, ...] (x + 1)  ==>  ?value

(A) 0

(B) 1

(C) Error

QUIZ

What is a suitable env such that

eval env (x + 1)   ==>   10

(A) []

(B) [x := 0, y := 9]

(C) [x := 9, y := 0]

(D) [x := 9, y := 10, z := 666]

(E) [y := 10, z := 666, x := 9]

Evaluating Variables

Using the above intuition, lets update our evaluator to handle variables i.e. the EVar case:

eval env (EVar x)        = ???

Lets confirm that our eval is ok!

envA = []
envB = ["x" := 0 , "y" := 9]
envC = ["x" := 9 , "y" := 0]
envD = ["x" := 9 , "y" := 10 , "z" := 666]
envE = ["y" := 10, "z" := 666, "x" := 9  ]

-- >>> eval envA (EBin Add (EVar "x") (ENum 1))
-- >>> eval envB (EBin Add (EVar "x") (ENum 1))
-- >>> eval envC (EBin Add (EVar "x") (ENum 1))
-- >>> eval envD (EBin Add (EVar "x") (ENum 1))
-- >>> eval envE (EBin Add (EVar "x") (ENum 1))

The Nano Language

Features of Nano:

1. Arithmetic expressions [done]
2. Variables [done]
3. Let-bindings
4. Functions
5. Recursion

2. Nano: Variables

Let’s add variables and let bindings!

e ::= n                   -- OLD
    | e1 + e2
    | e1 - e2
    | e1 * e2
    | x
                          -- NEW
    | let x = e1 in e2

Lets extend our datatype

type Id = String

data Expr
  = ENum Int              -- OLD
  | EBin Binop Expr Expr  
  | EVar Id
                         -- NEW
  | ELet Id Expr Expr

How should we extend eval ?

QUIZ

What should the following expression evaluate to?

let x = 0
in
  x + 1

(A) Error

(B) 1

(C) 0

QUIZ

What should the following expression evaluate to?

let x = 0
in
  let y = 100
  in
    x + y

(A) Error

(B) 0

(C) 1

(D) 100

(E) 101

QUIZ

What should the following expression evaluate to?

let x = 0
in
  let x = 100
  in
    x + 1

(A) Error

(B) 0

(C) 1

(D) 100

(E) 101

QUIZ

What should the following expression evaluate to?

let x = 0
in
  (let x = 100 in
   in
     x + 1
  )
  +
  x

(A) Error

(B) 1

(C) 101

(D) 102

(E) 2

Principle: Static/Lexical Scoping

Every variable use gets its value from a unique definition:

• “Nearest” let-binder in program text

“Static” means you can tell without running the program

Great for readability and debugging

1. Define local variables
2. Be sure where each variable got its value

Don’t have to scratch head to figure where a variable got “assigned”

How to implement static scoping?

QUIZ

Lets re-evaluate the quizzes!

              -- env
let x = 0
in            -- ??? what env to use for `x + 1`?
  x + 1

(A) env

(B) [ ]

(C) [ ("x" := 0) ]

(D) ("x" := 0) : env

(E) env ++ ["x" := 0]

QUIZ

                  -- env
let x = 0
in                  -- (x := 0) : env
  let y = 100
  in                  -- ??? what env to use for `x + y` ?
    x + y

(A) ("x" := 0) : env

(B) ("y" := 100) : env

(C) ("y" := 100) : ("x" := 0) : env

(D) ("x" := 0) : ("y" := 100) : env

(E) [("y" := 100), ("x" := 0)]

QUIZ

Lets re-evaluate the quizzes!

              -- env
let x = 0
in              -- ("x" := 0) : env
  let x = 100
  in              -- ??? what env to use for `x + 1`?
    x + 1

(A) ("x" := 0) : env

(B) ("x" := 100) : env

(C) ("x" := 100) : ("x" := 0) : env

(D) ("x" := 0) : ("x" := 100) : env

(E) [("x" := 100)]

Extending Environments

Lets fill in eval for the let x = e1 in e2 case!

eval env (ELet x e1 e2) = ???

1. Evaluate e1 in env to get a value v1
2. Extend environment with value for x i.e. to (x := v1) : env
3. Evaluate e2 using extended environment.

Lets make sure our tests pass!

Run-time Errors

Haskell function to evaluate an expression:

eval :: Env -> Expr -> Value
eval env (Num n)        = n
eval env (Var x)        = lookup x env      -- (A)
eval env (Bin op e1 e2) = evalOp op v1 v2   -- (B)
  where
    v1                  = eval env  e1      -- (C)
    v2                  = eval env  e2      -- (C) 
eval env (Let x e1 e2)  = eval env1 e2
  where
    v1                  = eval env e1
    env1                = (x, v1) : env     -- (D)

QUIZ

Will eval env expr always return a value ? Or, can it crash?

(A) operation at A may fail (B) operation at B may fail (C) operation at C may fail (D) operation at D may fail (E) nah, its all good…, always returns a Value

Free vs bound variables

Undefined Variables

How do we make sure lookup doesn’t cause a run-time error?

Bound Variables

Consider an expression let x = e1 in e2

• An occurrence of x is bound in e2

• i.e. when occurrence of form let x = ... in ... x ...

• i.e. when x occurs “under” a let binding for x.

Free Variables

An occurrence of x is free in e if it is not bound in e

Closed Expressions

An expression e is closed in environment env:

• If all free variables of e are defined in env

Successful Evaluation

lookup will never fail

• If eval env e is only called on e that is closed in env

QUIZ

Which variables occur free in the expression?

let y = (let x = 2
         in x      ) + x
in
  let x = 3
  in
    x + y

(A) None

(B) x

(C) y

(D) x and y

Exercise

Consider the function

evaluate :: Expr -> Value
evaluate e
  | isOk e    = eval emptyEnv e
  | otherwise = error "Sorry! bad expression, it will crash `eval`!"  
  where
    emptyEnv  = []               -- has NO bindings

What should isOk check for? (Try to implement it for nano…)

The Nano Language

Features of Nano:

1. Arithmetic expressions [done]
2. Variables [done]
3. Let-bindings [done]
4. Functions
5. Recursion

Nano: Functions

Let’s add

• lambda abstraction (aka function definitions)

• application (aka function calls)

e ::= n                   -- OLD
    | e1 `op` e2
    | x
    | let x = e1 in e2
                          -- NEW
    | \x -> e             -- abstraction
    | e1 e2               -- application

Example

let incr = \x -> x + 1
in
   incr 10

Representation

data Expr
  = ENum Int              -- OLD
  | EBin Binop Expr Expr  
  | EVar Id
  | ELet Id Expr Expr
                         -- NEW
  | ???                  -- abstraction \x -> e
  | ???                  -- application (e1 e2)

Representation

data Expr
  = ENum Int              -- OLD
  | EBin Binop Expr Expr  
  | EVar Id
  | ELet Id Expr Expr
                         -- NEW
  | ELam Id Expr         -- abstraction \x -> e
  | EApp Expr Expr       -- application (e1 e2)

Example

let incr = \x -> x + 1
in
   incr 10

is represented as

ELet "incr" (ELam "x" (EBin Add (EVar "x") (ENum 1)))
  (
    EApp (EVar "incr") (ENum 10)
  )

Functions are Values

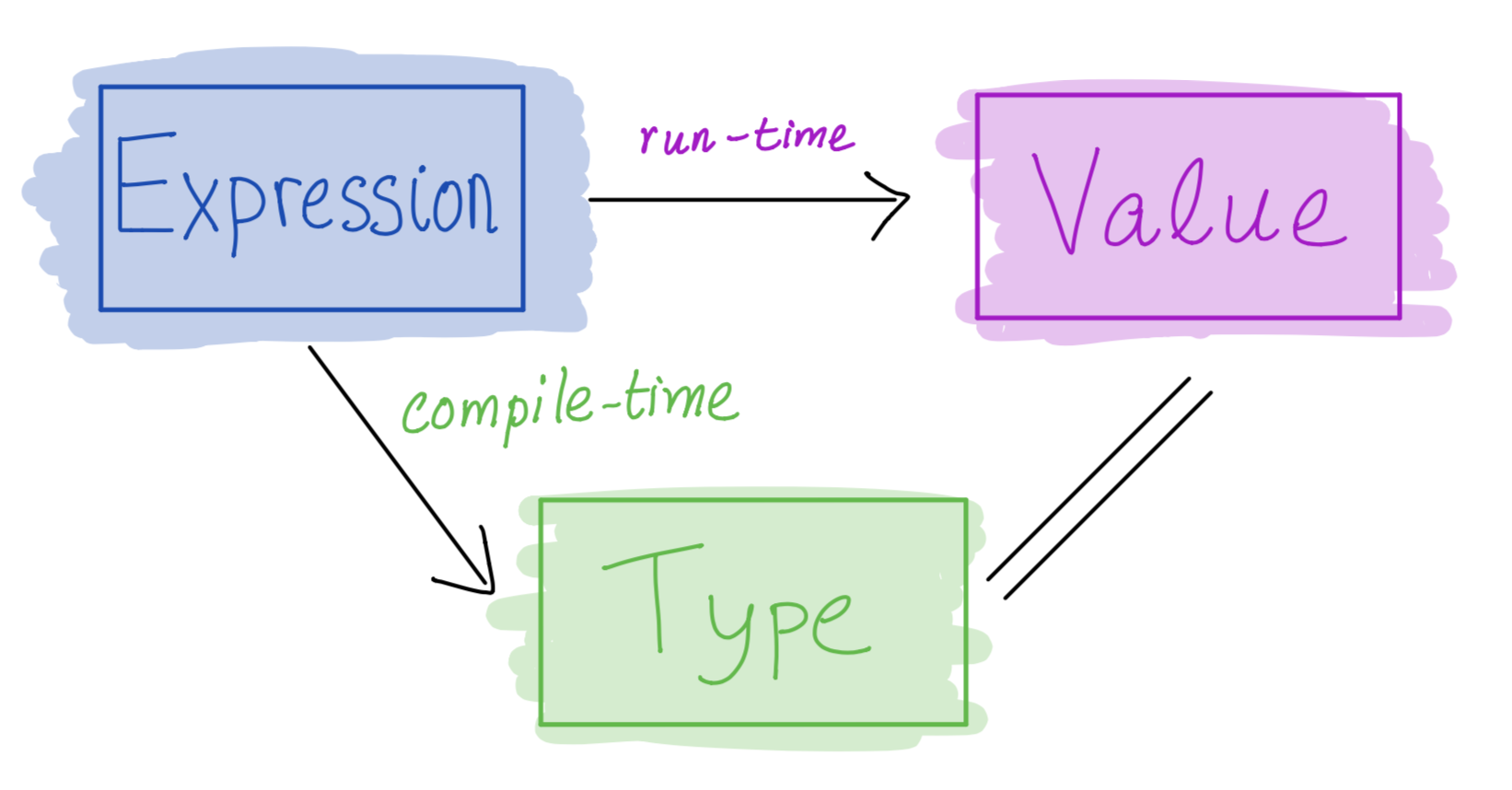
Recall the trinity

But… what is the value of a function?

Lets build some intuition with examples.

QUIZ

What does the following expression evaluate to?

let incr = \x -> x + 1    -- abstraction ("definition")
in
   incr 10                -- application ("call")

(A) Error/Undefined

(B) 10

(C) 11

(D) 0

(E) 1

What is the Value of incr?

• Is it an Int ?

• Is it a Bool ?

• Is it a ???

What information do we need to store (in the Env) about incr?

A Function’s Value is its Code

                        -- env
let incr = \x -> x + 1
in                      -- ("incr" := <code>) : env
    incr 10             -- evaluate <code> with parameter := 10

What information do we store about <code> ?

A Call’s Value

How to evaluate the “call” incr 10 ?

1. Lookup the <code> i.e. <param, body> for incr (stored in the environment),

2. Evaluate body with param set to 10!

Two kinds of Values

We now have two kinds of Values

v ::= n               -- OLD
    | <x, e>          -- <param, body>

1. Plain Int (as before)
2. A function’s “code”: a pair of “parameter” and “body-expression”

data Value
  = VInt  Int          -- OLD
  | VCode Id Expr      -- <x, e>

Evaluating Lambdas and Applications

eval :: Env -> Expr -> Value
                                -- OLD
eval env (ENum n)        = ???
eval env (EVar x)        = ???
eval env (EBin op e1 e2) = ???
eval env (ELet x  e1 e2) = ???
                                -- NEW
eval env (ELam x e)      = ???
eval env (EApp e1 e2)    = ???

Lets make sure our tests work properly!

exLam1 = ELet "incr" (ELam "x" (EBin Add (EVar "x") (ENum 1)))
          (
            EApp (EVar "incr") (ENum 10)
          )

-- >>> eval [] exLam1
-- 11

QUIZ

What should the following evaluate to?

let c = 1
in
   let inc = \x -> x + c
   in
      inc 10

(A) Error/Undefined

(B) 10

(C) 11

(D) 0

(E) 1

exLam2 = ELet "c" (ENum 1)
           (ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
              (
              EApp (EVar "incr") (ENum 10)
              )
           )

-- >>> eval [] exLam2
-- ???

QUIZ

And what should this expression evaluate to?

let c = 1
in
   let inc = \x -> x + c
   in
      let c = 100
      in
        inc 10

(A) Error/Undefined

(B) 110

(C) 11

The “Immutability Principle”

A function’s behavior should never change

• A function must always return the same output for a given input

Why?

> myFunc 10
0

> myFunc 10
10

Oh no! How to find the bug? Is it

• In myFunc or
• In a global variable or
• In a library somewhere else or
• …

My worst debugging nightmare

Colbert “Immutability Principle”

The Immutability Principle ?

How does our eval work?

exLam3 = ELet "c" (ENum 1)
           (
           ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
              (
               ELet "c" (ENum 100)
                 (
                 EApp (EVar "incr") (ENum 10)
                 )
              )
           )

-- >>> eval [] exLam3
-- ???

Oops?

                          -- []
let c = 1
in                        -- ["c" := 1]
   let inc = \x -> x + c
   in                     -- ["inc" := <x, x+c>, c := 1]
      let c = 100
      in                  -- ["c" := 100, "inc" := <x, x+c", "c" := 1]   <<< env
        inc 10

And so we get

eval env (inc 10)

  ==> eval ("x" := 10 : env) (x + c)

  ==> 10 + 100

  ==> 110

Ouch.

Enforcing Immutability with Closures

How to enforce immutability principle

• inc 10 always returns 11?

Key Idea: Closures

At definition: Freeze the environment the function’s value

At call: Use the frozen environment to evaluate the body

Ensures that inc 10 always evaluates to the same result!

                          -- []
let c = 1
in                        -- ["c" := 1]
   let inc = \x -> x + c
   in                     -- ["inc" := <frozenv, x, x+c>, c := 1]  <<< frozenv = ["c" := 1]
      let c = 100
      in                  -- ["c" := 100, "inc" := <frozenv, x, x+c>, "c" := 1]
        inc 10

Now we evaluate

eval env (inc 10)

  ==> eval ("x" := 10 : frozenv) (x + c)  where frozenv = ["c" := 1]

  ==> 10 + 1

  ==> 1

tada!

Representing Closures

Lets change the Value datatype to also store an Env

data Value
  = VInt  Int          -- OLD
  | VClos Env Id Expr  -- <frozenv, param, body>  

Evaluating Function Definitions

How should we fix the definition of eval for ELam?

eval :: Env -> Expr -> Value

eval env (ELam x e) = ???

Hint: What value should we bind incr to in our example above?

(Recall At definition freeze the environment the function’s value)

Evaluating Function Calls

How should we fix the definition of eval for EApp?

eval :: Env -> Expr -> Value

eval env (EApp e1 e2) = ???

(Recall At call: Use the frozen environment to evaluate the body)

Hint: What value should we evaluate incr 10 to?

1. Evaluate incr to get <frozenv, "x", x + c>
2. Evaluate 10 to get 10
3. Evaluate x + c in x:=10 : frozenv

Let’s generalize that recipe!

1. Evaluate e1 to get <frozenv, param, body>
2. Evaluate e2 to get v2
3. Evaluate body in param := v2 : frozenv

Immutability Achieved

Lets put our code to the test!

exLam3 = ELet "c" (ENum 1)
           (
           ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
              (
               ELet "c" (ENum 100)
                 (
                 EApp (EVar "incr") (ENum 10)
                 )
              )
           )

-- >>> eval [] exLam3
-- ???

QUIZ

What should the following evaluate to?

let add = \x -> (\y -> x + y)
in
  let add10 = add 10
  in
    let add20 = add 20
    in 
      (add10 100) + (add20 1000)

TODO

Functions Returning Functions Achieved!

exLam4 = ...

-- >>> eval [] exLam4

TODO

Practice

What should the following evaluate to?

let add = \x -> (\y -> x + y)
in
  let add10 = add 10
  in
    let doTwice = \f -> (\x -> f (f x))
    in
      doTwice add10 100

Functions Accepting Functions Achieved!

exLam5 = ...

-- >>> eval [] exLam4

The Nano Language

Features of Nano:

1. Arithmetic expressions [done]
2. Variables [done]
3. Let-bindings [done]
4. Functions [done]
5. Recursion

… You figure it out Hw4 … :-)