From the Lambda Calculus to Haskell
What is Haskell?
A typed, lazy, purely functional programming language
Haskell = λ-calculus ++
- better syntax
- types
- built-in features
- booleans, numbers, characters
- records (tuples)
- lists
- recursion
- …
Programming in Haskell
Computation by Calculation
Substituting equals by equals
Computation via Substituting Equals by Equals
(1 + 3) * (4 + 5)
-- subst 1 + 3 = 4
==> 4 * (4 + 5)
-- subst 4 + 5 = 9
==> 4 * 9
-- subst 4 * 9 = 36
==> 36
Computation via Substituting Equals by Equals
Equality-Substitution enables Abstraction via Pattern Recognition
Abstraction via Pattern Recognition
Repeated Expressions
31 * (42 + 56)
70 * (12 + 95)
90 * (68 + 12)Recognize Pattern as λ-function
pat = \x y z -> x * ( y + z ) Equivalent Haskell Definition
pat x y z = x * ( y + z ) Function Call is Pattern Instance
pat 31 42 56 =*> 31 * (42 + 56) =*> 31 * 98 =*> 3038
pat 70 12 95 =*> 70 * (12 + 95) =*> 70 * 107 =*> 7490
pat 90 68 12 =*> 90 * (68 + 12) =*> 90 * 80 =*> 7200Key Idea: Computation is substitute equals by equals.
Programming in Haskell
Substitute Equals by Equals
Thats it! (Do not think of registers, stacks, frames etc.)
Elements of Haskell
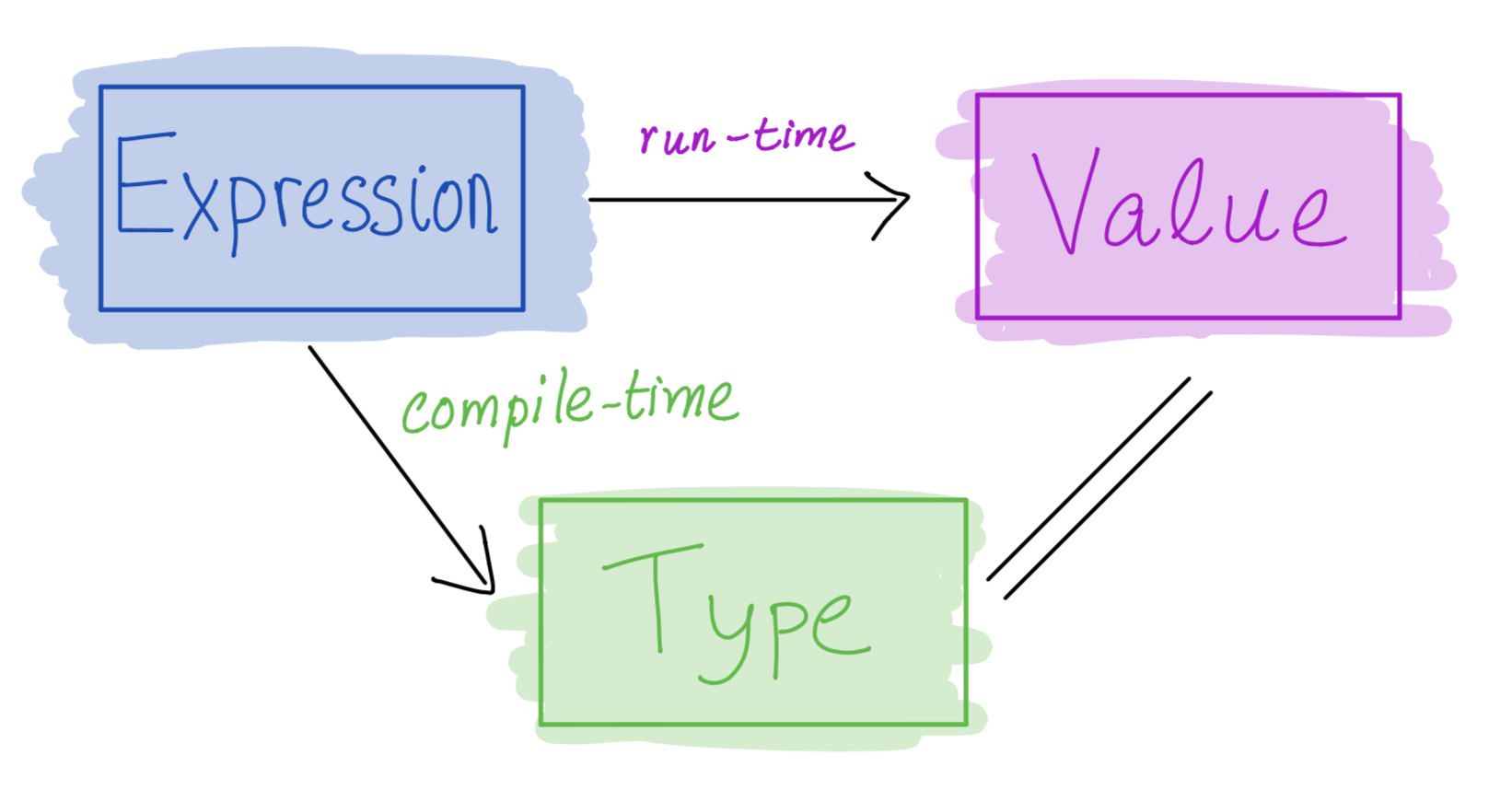
- Core program element is an expression
- Every valid expression has a type (determined at compile-time)
- Every valid expression reduces to a value (computed at run-time)
Ill-typed* expressions are rejected at compile-time before execution
- like in Java
- not like λ-calculus or Python …
weirdo = 1 0 -- rejected by GHC
Why are types good?
- Helps with program design
- Types are contracts (ignore ill-typed inputs!)
- Catches errors early
- Allows compiler to generate code
- Enables compiler optimizations
The Haskell Eco-System
Batch compiler:
ghcCompile and run large programsInteractive Shell
ghciShell to interactively run small programs onlineBuild Tool
stackBuild tool to manage libraries etc.
Interactive Shell: ghci
$ stack ghci
:load file.hs
:type expression
:info variable
A Haskell Source File
A sequence of top-level definitions x1, x2, …
Each has type
type_1,type_2, …Each defined by expression
expr_1,expr_2, …
x_1 :: type_1
x_1 = expr_1
x_2 :: type_2
x_2 = expr_2
.
.
.
Basic Types
ex1 :: Int
ex1 = 31 * (42 + 56) -- this is a comment
ex2 :: Double
ex2 = 3 * (4.2 + 5.6) -- arithmetic operators "overloaded"
ex3 :: Char
ex3 = 'a' -- 'a', 'b', 'c', etc. built-in `Char` values
ex4 :: Bool
ex4 = True -- True, False are builtin Bool values
ex5 :: Bool
ex5 = False
QUIZ: Basic Operations
ex6 :: Int
ex6 = 4 + 5
ex7 :: Int
ex7 = 4 * 5
ex8 :: Bool
ex8 = 5 > 4
quiz :: ???
quiz = if ex8 then ex6 else ex7What is the type of quiz?
A. Int
B. Bool
C. Error!
QUIZ: Basic Operations
ex6 :: Int
ex6 = 4 + 5
ex7 :: Int
ex7 = 4 * 5
ex8 :: Bool
ex8 = 5 > 4
quiz :: ???
quiz = if ex8 then ex6 else ex7What is the value of quiz?
A. 9
B. 20
C. Other!
Function Types
In Haskell, a function is a value that has a type
A -> BA function that
- takes input of type
A - returns output of type
B
For example
isPos :: Int -> Bool
isPos = \n -> (x > 0)Define function-expressions using \ like in λ-calculus!
But Haskell also allows us to put the parameter on the left
isPos :: Int -> Bool
isPos n = (x > 0)(Meaning is identical to above definition with \n -> ...)
Multiple Argument Functions
A function that
- takes three inputs
A1,A2andA3 - returns one output
Bhas the type
A1 -> A2 -> A3 -> BFor example
pat :: Int -> Int -> Int -> Int
pat = \x y z -> x * (y + z)which we can write with the params on the left as
pat :: Int -> Int -> Int -> Int
pat x y z = x * (y + z)
QUIZ
What is the type of quiz ?
quiz :: ???
quiz x y = (x + y) > 0A. Int -> Int
B. Int -> Bool
C. Int -> Int -> Int
D. Int -> Int -> Bool
E. (Int, Int) -> Bool
Function Calls
A function call is exactly like in the λ-calculus
e1 e2where e1 is a function and e2 is the argument. For example
>>> isPos 12
True
>>> isPos (0 - 5)
False
Multiple Argument Calls
With multiple arguments, just pass them in one by one, e.g.
(((e e1) e2) e3)For example
>>> pat 31 42 56
3038
EXERCISE
Write a function myMax that returns the maximum of two inputs
myMax :: Int -> Int -> Int
myMax = ???When you are done you should see the following behavior:
>>> myMax 10 20
20
>>> myMax 100 5
100
EXERCISE
Write a function sumTo such that sumTo n evaluates to 0 + 1 + 2 + ... + n
sumTo :: Int -> Int
sumTo n = ???When you are done you should see the following behavior:
>>> sumTo 3
6
>>> sumTo 4
10
>>> sumTo 5
15
How to Return Multiple Outputs?
Tuples
A type for packing n different kinds of values into a single “struct”
(T1,..., Tn)For example
tup1 :: ???
tup1 = ('a', 5)
tup2 :: (Char, Double, Int)
tup2 = ('a', 5.2, 7)
QUIZ
What is the type ??? of tup3?
tup3 :: ???
tup3 = ((7, 5.2), True)A. (Int, Bool)
B. (Int, Double, Bool)
C. (Int, (Double, Bool))
D. ((Int, Double), Bool)
E. (Tuple, Bool)
Extracting Values from Tuples
We can create a tuple of three values e1, e2, and e3 …
tup = (e1, e2, e3)… but how to extract the values from this tuple?
Pattern Matching via case-of expressions
fst3 :: (t1, t2, t3) -> t1
fst3 t = case t of
(x1, x2, x3) -> x1
snd3 :: (t1, t2, t3) -> t2
snd3 t = case t of
(x1, x2, x3) -> x2
thd3 :: (t1, t2, t3) -> t3
thd3 t = case t of
(x1, x2, x3) -> x3
QUIZ
What is the value of quiz defined as
tup2 :: (Char, Double, Int)
tup2 = ('a', 5.2, 7)
snd3 :: (t1, t2, t3) -> t2
snd3 t = case t of
(x1, x2, x3) -> x2
quiz = snd3 tup2A. 'a'
B. 5.2
C. 7
D. ('a', 5.2)
E. (5.2, 7)
Lists
Unbounded Sequence of values of type T
[T]For example
chars :: [Char]
chars = ['a', 'b', 'c']
ints :: [Int]
ints = [1, 3, 5, 7]
pairs :: [(Int, Bool)]
pairs = [(1,True), (2,False)]
QUIZ
What is the type of things defined as
things :: ???
things = [ [1], [2, 3], [4, 5, 6] ] A. [Int]
B. ([Int], [Int], [Int])
C. [(Int, Int, Int)]
D. [[Int]]
E. List
List’s Values Must Have The SAME Type!
The type [T] denotes an unbounded sequence of values of type T
Suppose you have a list
oops = [1, 2, 'c']There is no T that we can use
- As last element is not
Int - First two elements are not
Char!
Result: Mysterious Type Error!
Constructing Lists
There are two ways to construct lists
[] -- creates an empty list
h:t -- creates a list with "head" 'h' and "tail" t For example
>>> 3 : []
[3]
>>> 2 : (3 : [])
[2, 3]
>>> 1 : (2 : (3 : []))
[1, 2, 3]Cons Operator : is Right Associative
x1 : x2 : x3 : x4 : t means x1 : (x2 : (x3 : (x4 : t)))
So we can just avoid the parentheses.
Syntactic Sugar
Haskell lets you write [x1, x2, x3, x4] instead of x1 : x2 : x3 : x4 : []
Functions Producing Lists
Lets write a function copy3 that
- takes an input
xand - returns a list with three copies of
x
copy3 :: ???
copy3 x = ???When you are done, you should see the following
>>> copy3 5
[5, 5, 5]
>>> copy3 "cat"
["cat", "cat", "cat"]
Lets write some Functions
Step 1: Write some tests
Step 2: Write the type
Step 3: Write the code
PRACTICE: Clone
Write a function clone such that clone n x returns a list with n copies of x.
1. Tests
When you are done you should see the following behavior
>>> clone 0 "cat"
[]
>>> clone 1 "cat"
["cat"]
>>> clone 2 "cat"
["cat", "cat"]
>>> clone 3 "cat"
["cat", "cat", "cat"]
>>> clone 3 100
[100, 100, 100]2. Types
clone :: ???3. Code
clone n x = ???
How does clone execute?
(Substituting equals-by-equals!)
clone 3 100
=*> ???
EXERCISE: Range
Write a function range such that range i j returns the list of values [i, i+1, ..., j]
range :: ???
range i j = ???1. Tests
>>> range 4 3
[]
>>> range 3 3
[3]
>>> range 2 3
[2, 3]
>>> range 1 3
[1, 2, 3]
>>> range 0 3
[0, 1, 2, 3]2. Type
range :: ???3. Code
range = ???
Functions Consuming Lists
So far: how to produce lists.
Next how to consume lists!
EXERCISE
Lets write a function firstElem such that firstElem xs returns the first element xs if it is a non-empty list, and 0 otherwise.
HINT: How to extract values from a list?
1. Tests
When you are done you should see the following behavior:
>>> firstElem []
0
>>> firstElem [10, 20, 30]
10
>>> firstElem [5, 6, 7, 8]
52. Type
firstElem :: ???3. Code
firstElem = ???
QUIZ
Suppose we have the following mystery function
mystery :: [a] -> Int
mystery l = case l of
[] -> 0
(x:xs) -> 1 + mystery xsWhat does mystery [10, 20, 30] evaluate to?
A. 10
B. 20
C. 30
D. 3
E. 0
EXERCISE: Summing a List
Write a function sumList such that sumList [x1, ..., xn] returns x1 + ... + xn
1. Tests
When you are done you should get the following behavior:
>>> sumList []
0
>>> sumlist [3]
3
>>> sumlist [2, 3]
5
>>> sumlist [1, 2, 3]
62. Type
sumList :: [Int] -> Int3. Code
sumList = ???Functions on lists: take
Let’s write a function to take first n elements of a list xs.
1. Tests
-- >>> ???2. Type
take :: ???Some useful library functions
-- | Length of the list
length :: [t] -> Int
-- | Append two lists
(++) :: [t] -> [t] -> [t]
-- | Are two lists equal?
(==) :: [t] -> [t] -> BoolYou can search for library functions on Hoogle!
**3. Code**
```haskell
take = ???Some useful library functions
-- | Length of the list
length :: [t] -> Int
-- | Append two lists
(++) :: [t] -> [t] -> [t]
-- | Are two lists equal?
(==) :: [t] -> [t] -> BoolYou can search for library functions on Hoogle!
Recap

- Core program element is an expression
- Every valid expression has a type (determined at compile-time)
- Every valid expression reduces to a value (computed at run-time)
Execution
Basic values & operators
Execution / Function Calls just substitute equals by equals
Pack data into tuples & lists
Unpack data via pattern-matching
