Plan for this week

Last week:

• built-in data types
  • base types, tuples, lists (and strings)
• writing functions using pattern matching and recursion

This week:

• user-defined data types
  • and how to manipulate them using pattern matching and recursion
• more details about recursion

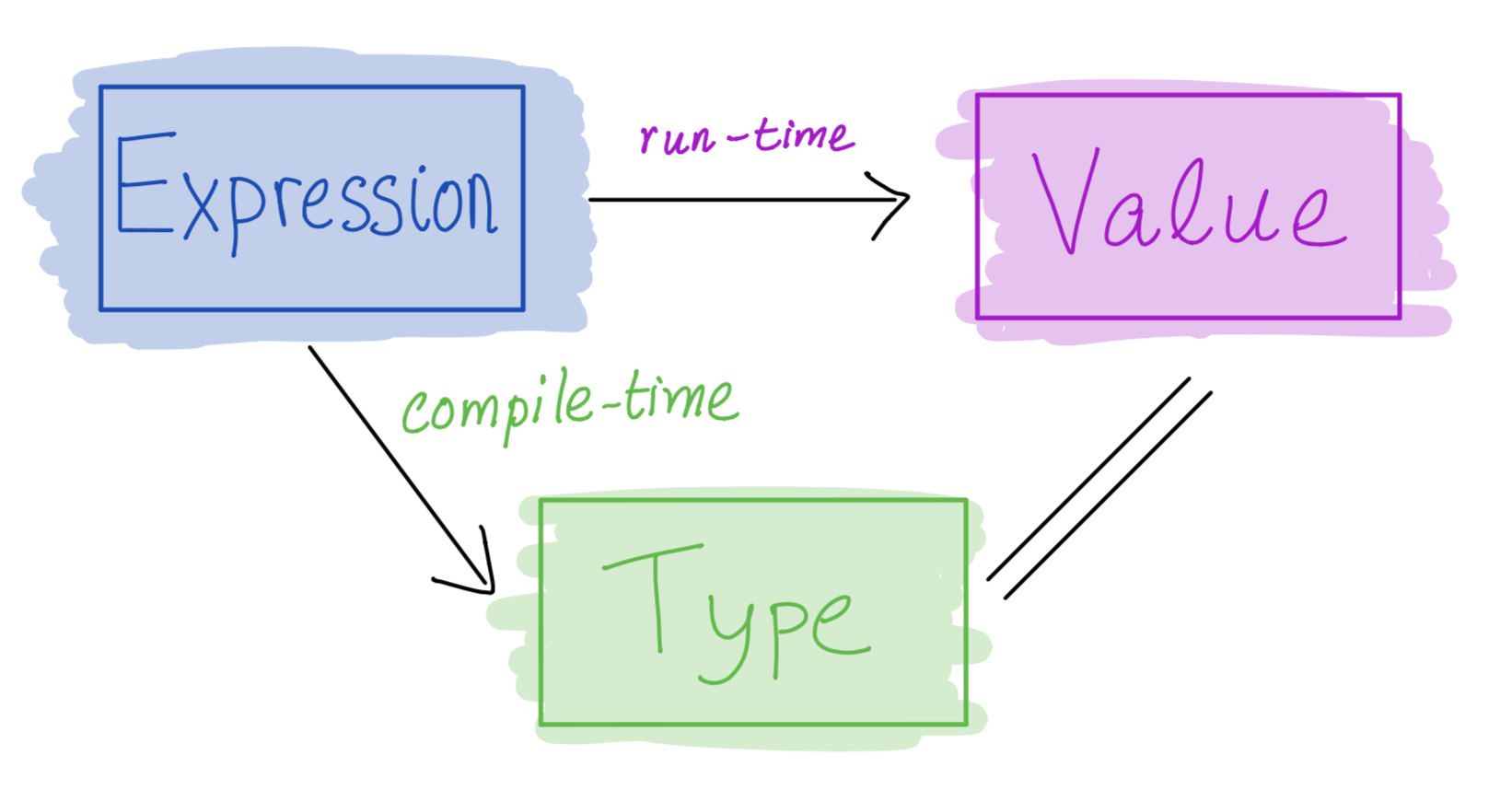
Representing complex data

Previously, we’ve seen:

• base types: Bool, Int, Integer, Float

• some ways to build up types: given types T1, T2

  • functions: T1 -> T2
  • tuples: (T1, T2)
  • lists: [T1]

Next: Algebraic Data Types:

A single, powerful way to type complex data

• Lets you define your own data types

• Tuples and lists are special cases

Building data types

Three key ways to build complex types/values:

1. Product types (each-of): a value of T contains a value of T1 and a value of T2

2. Sum types (one-of): a value of T contains a value of T1 or a value of T2

3. Recursive types: a value of T contains a sub-value of the same type T

Product types

Tuples can do the job but there are two problems…

deadlineDate :: (Int, Int, Int)
deadlineDate = (1, 28, 2022)

deadlineTime :: (Int, Int, Int)
deadlineTime = (11, 59, 59)

-- | Deadline date extended by one day
extendDate :: (Int, Int, Int) -> (Int, Int, Int)
extendDate = ...

Can you spot them?

1. Verbose and unreadable

A type synonym for T: a name that can be used interchangeably with T

type Date = (Int, Int, Int)
type Time = (Int, Int, Int)

deadlineDate :: Date
deadlineDate = (1, 28, 2021)

deadlineTime :: Time
deadlineTime = (11, 59, 59)

-- | Deadline date extended by one day
extendDate :: Date -> Date
extendDate = ...

2. Unsafe

We want to catch this error at compile time!!!

extension deadlineTime

Solution: construct two different datatypes

data Date    = Date Int Int Int
data Time    = Time Int Int Int
                 ^    ^---^---^---- parameter types
                 `---------------- constructor name

deadlineDate :: Date
deadlineDate = Date 2 7 2020

deadlineTime :: Time
deadlineTime = Time 11 59 59

Record syntax

Haskell’s record syntax allows you to name the constructor parameters:

• Instead of

  data Date = Date Int Int Int

• you can write:

  data Date = Date
    { month :: Int
    , day   :: Int
    , year  :: Int  
    }

• then you can do:

  deadlineDate = Date 2 4 2019
  
  deadlineMonth = month deadlineDate -- use field name as a function

Building data types

Three key ways to build complex types/values:

1. Product types (each-of): a value of T contains a value of T1 and a value of T2 [done]

2. Sum types (one-of): a value of T contains a value of T1 or a value of T2

3. Recursive types: a value of T contains a sub-value of the same type T

Example: NanoMarkdown

Suppose I want to represent a text document with simple markup

Each paragraph is either:

• plain text (String)
• heading: level and text (Int and String)
• list: ordered? and items (Bool and [String])

I want to store all paragraphs in a list

doc = [ (1, "Notes from 130")                   -- Level 1 heading
      , "There are two types of languages:"     -- Plain text
      , (True, [ "those people complain about"  -- Ordered list
               , "those no one uses"])
      ]

But this does not type check!!!

Sum Types

Solution: construct a new type for paragraphs that is a sum (one-of) the three options!

Each paragraph is either:

• plain text (String)
• heading: level and text (Int and String)
• list: ordered? and items (Bool and [String])

data Paragraph              -- ^ THREE constructors, w/ different parameters
  = PText    String         -- ^ text: plain string
  | PHeading Int   String   -- ^ head: level and text (Int & String)
  | PList    Bool [String]  -- ^ list: ordered? & items (Bool & [String])

QUIZ

data Paragraph
  = PText String
  | PHeading Int String
  | PList Bool [String]

What is the type of Text "Hey there!"? i.e. How would GHCi reply to:

>:t (PText "Hey there!")

A. Syntax error

B. Type error

C. PText

D. String

E. Paragraph

Constructing datatypes

data T
  = C1 T11 ... T1k
  | C2 T21 ... T2l
  | ... 
  | Cn Tn1 ... Tnm

• T is the new datatype

• C1 .. Cn are the constructors of T

A value of type T is

• either C1 v1 .. vk with vi :: T1i
• or C2 v1 .. vl with vi :: T2i
• or …
• or Cn v1 .. vm with vi :: Tni

You can think of a T value as a box:

• either a box labeled C1 with values of types T11 .. T1k inside
• or a box labeled C2 with values of types T21 .. T2l inside
• or …
• or a box labeled Cn with values of types Tn1 .. Tnm inside

Constructing datatypes: Paragraph

data Paragraph
  = PText String
  | PHeading Int String
  | PList Bool [String]

Apply a constructor = pack some values into a box (and label it)

• PText "Hey there!"
  • put "Hey there!" in a box labeled PText
• PHeading 1 "Introduction"
  • put 1 and "Introduction" in a box labeled PHeading
• Boxes have different labels but same type (Paragraph)

with example values:

QUIZ

data Paragraph
  = PText String
  | PHeading Int String
  | PList Bool [String]

What would GHCi say to

>:t [PHeading 1 "Introduction", PText "Hey there!"]

A. Syntax error

B. Type error

C. Paragraph

D. [Paragraph]

E. [String]

Example: NanoMD

data Paragraph
  = PText String
  | PHeading Int String
  | PList Bool [String]

Now I can create a document like so:

doc :: [Paragraph]
doc = [ PHeading 1 "Notes from 130"
      , PText "There are two types of languages:"
      , PList True [ "those people complain about"
                   , "those no one uses"
                   ])
      ]

Problem: How to Convert Documents to HTML?

How to write a function

html :: Paragraph -> String
html p = ???      -- ^ depends on the kind of paragraph!

How to tell what’s in the box?

• Look at the label!

Pattern matching

Pattern matching = looking at the label and extracting values from the box

• we’ve seen it before
• but now for arbitrary datatypes

html :: Paragraph -> String
html p = case p of
           PText str        -> ...  -- It's a plain text; str :: String 
           PHeading lvl str -> ...  -- It's a heading;    lvl :: Int, str :: String
           PList ord items  -> ...  -- It's a list;       ord :: Bool, items :: [String]

or, we can pull the case-of to the “top” as

html :: Paragraph -> String
html (PText str)        = ...  -- It's a plain text; str :: String 
html (PHeading lvl str) = ...  -- It's a heading;    lvl :: Int, str :: String
html (PList ord items)  = ...  -- It's a list;       ord :: Bool, items :: [String]

html :: Paragraph -> String
html (PText str)            -- It's a plain text! Get string
  = unlines [open "p", str, close "p"]

html (PHeading lvl str)     -- It's a heading! Get level and string
  = let htag = "h" ++ show lvl
    in unwords [open htag, str, close htag]

html (PList ord items)      -- It's a list! Get ordered and items
  = let ltag   = if ord then "ol" else "ul"
        litems = [unwords [open "li", i, close "li"] | i <- items]
    in unlines ([open ltag] ++ litems ++ [close ltag])

Dangers of pattern matching (1)

html :: Paragraph -> String
html (PText str) = ...
html (PList ord items) = ...

What would GHCi say to:

html (PHeading 1 "Introduction")

Dangers of pattern matching (2)

html :: Paragraph -> String
html (PText str)        = unlines [open "p", str, close "p"]
html (PHeading lvl str) = ...
html (PHeading 0 str)   = html (PHeading 1 str)
html (PList ord items)  = ...

What would GHCi say to:

html (PHeading 0 "Introduction")

Dangers of pattern matching

Beware of missing and overlapped patterns

• GHC warns you about overlapped patterns
• GHC warns you about missing patterns when called with -W (use :set -W in GHCi)

Pattern-Match Expression

Everything is an expression?

We’ve seen: pattern matching in equations

Actually, pattern-match is also an expression

html :: Paragraph -> String
html p = case p of
           PText    str       -> unlines [open "p", str, close "p"]
           PHeading lvl str   -> ...
           PList    ord items -> ...

The code we saw earlier was syntactic sugar

html (C1 x1 ...) = e1
html (C2 x2 ...) = e2
html (C3 x3 ...) = e3

is just for humans, internally represented as a case-of expression

html p = case p of
           (C1 x1 ...) -> e1
           (C2 x2 ...) -> e2
           (C3 x3 ...) -> e3

QUIZ

What is the type of

let p = Text "Hey there!"
in case p of
    PText    str   -> str
    PHeading lvl _ -> lvl
    PList    ord _ -> ord

A. Syntax error

B. Type error

C. String

D. Paragraph

E. Paragraph -> String

Pattern matching expression: typing

The case expression

case e of
  pattern1 -> e1
  pattern2 -> e2
  ...
  patternN -> eN

has type T if

• each e1…eN has type T
• e has some type D
• each pattern1…patternN is a valid pattern for D
  • i.e. a variable or a constructor of D applied to other patterns

The expression e is called the match scrutinee

QUIZ

What is the type of

let p = Text "Hey there!"
in case p of
    PText _      -> 1
    PHeading _ _ -> 2
    PList _ _    -> 3

A. Syntax error

B. Type error

C. Paragraph

D. Int

E. Paragraph -> Int

Building data types

Three key ways to build complex types/values:

1. Product types (each-of): a value of T contains a value of T1 and a value of T2 [done]

   • Cartesian product of two sets: v(T) = v(T1) × v(T2)

2. Sum types (one-of): a value of T contains a value of T1 or a value of T2 [done]

   • Union (sum) of two sets: v(T) = v(T1) ∪ v(T2)

3. Recursive types: a value of T contains a sub-value of the same type T

Recursive types

Let’s define natural numbers from scratch:

data Nat = ???

data Nat = Zero | Succ Nat

A Nat value is:

• either an empty box labeled Zero
• or a box labeled Succ with another Nat in it!

Some Nat values:

Zero                     -- 0
Succ Zero                -- 1
Succ (Succ Zero)         -- 2
Succ (Succ (Succ Zero))  -- 3
...

Functions on recursive types

Recursive code mirrors recursive data

1. Recursive type as a parameter

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

Step 1: add a pattern per constructor

toInt :: Nat -> Int
toInt Zero     = ... -- base case
toInt (Succ n) = ... -- inductive case
                     -- (recursive call goes here)

Step 2: fill in base case:

toInt :: Nat -> Int
toInt Zero     = 0   -- base case
toInt (Succ n) = ... -- inductive case
                     -- (recursive call goes here)

Step 2: fill in inductive case using a recursive call:

toInt :: Nat -> Int
toInt Zero     = 0           -- base case
toInt (Succ n) = 1 + toInt n -- inductive case

QUIZ

What does this evaluate to?

let foo i = if i <= 0 then Zero else Succ (foo (i - 1))
in foo 2 

A. Syntax error

B. Type error

C. 2

D. Succ Zero

E. Succ (Succ Zero)

2. Recursive type as a result

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

         
fromInt :: Int -> Nat
fromInt n
  | n <= 0    = Zero                   -- base case
  | otherwise = Succ (fromInt (n - 1)) -- inductive case
                                       -- (recursive call goes here)

EXERCISE: Putting the two together

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

         
add :: Nat -> Nat -> Nat
add n m = ???

sub :: Nat -> Nat -> Nat
sub n m = ???

EXERCISE: Putting the two together

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

         
add :: Nat -> Nat -> Nat
add n m = ???

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

         
add :: Nat -> Nat -> Nat
add Zero     m = ???            -- base case
add (Succ n) m = ???            -- inductive case

EXERCISE: Putting the two together

data Nat = Zero     -- base constructor
         | Succ Nat -- inductive constructor

sub :: Nat -> Nat -> Nat
sub n m = ???

sub :: Nat -> Nat -> Nat
sub n        Zero     = ???     -- base case 1
sub Zero     _        = ???     -- base case 2
sub (Succ n) (Succ m) = ???     -- inductive case

Lesson: Recursive code mirrors recursive data

• Which of multiple arguments should you recurse on?

• Key: Pick the right inductive strategy!

(easiest if there is a single argument of course…)

Example: Calculator

I want to implement an arithmetic calculator to evaluate expressions like:

• 4.0 + 2.9
• 3.78 – 5.92
• (4.0 + 2.9) * (3.78 - 5.92)

What is a Haskell datatype to represent these expressions?

data Expr = ???

data Expr = Num Float
          | Add Expr Expr
          | Sub Expr Expr
          | Mul Expr Expr

We can represent expressions as

e0, e1, e2 :: Expr
e0 = Add (Num 4.0)  (Num 2.9)
e1 = Sub (Num 3.78) (Num 5.92)
e2 = Mul e0 e1

EXERCISE: Expression Evaluator

Write a function to evaluate an expression.

-- >>> eval (Add (Num 4.0)  (Num 2.9))
-- 6.9

eval :: Expr -> Float
eval e = ???

Recursion is…

Building solutions for big problems from solutions for sub-problems

• Base case: what is the simplest version of this problem and how do I solve it?
• Inductive strategy: how do I break down this problem into sub-problems?
• Inductive case: how do I solve the problem given the solutions for subproblems?

Lists

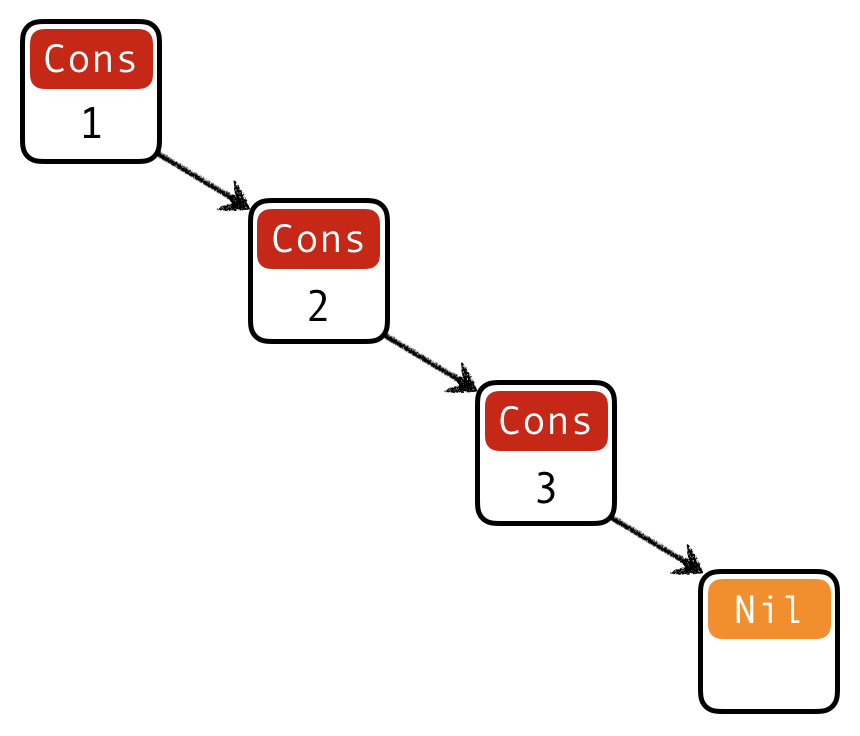
Lists aren’t built-in! They are an algebraic data type like any other:

data List 
  = Nil           -- ^ base constructor
  | Cons Int List -- ^ inductive constructor

• List [1, 2, 3] is represented as Cons 1 (Cons 2 (Cons 3 Nil))

• Built-in list constructors [] and (:) are just fancy syntax for Nil and Cons

Functions on lists follow the same general strategy:

length :: List -> Int
length Nil         = 0              -- base case
length (Cons _ xs) = 1 + length xs  -- inductive case

EXERCISE: Appending Lists

What is the right inductive strategy for appending two lists?

-- >>> append (Cons 1 (Cons 2 (Cons 3 Nil))) (Cons 4 (Cons 5 (Cons 6 Nil)))
-- (Cons 1 (Cons 2 (Cons 3 (Cons 4 (Cons 5 (Cons 6 Nil))))))

append :: List -> List -> List
append xs ys = ??

Trees

Lists are unary trees with elements stored in the nodes:

data List = Nil | Cons Int List

How do we represent binary trees with elements stored in the nodes?

QUIZ: Binary trees I

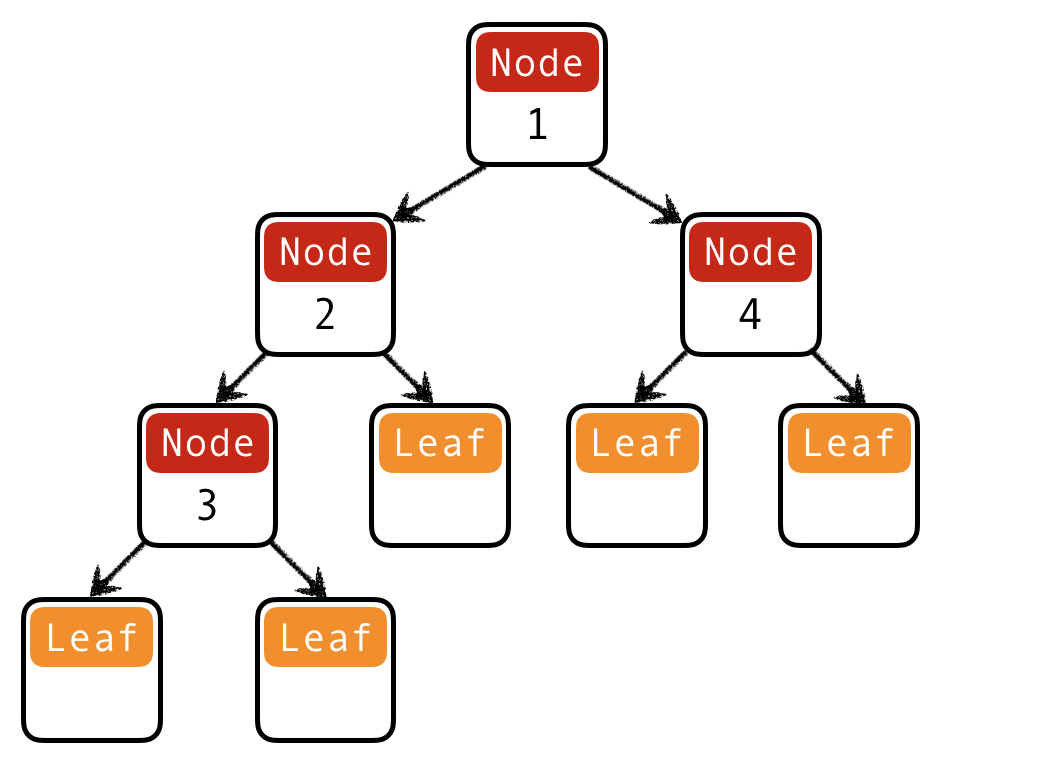
What is a Haskell datatype for binary trees with elements stored in the nodes?

(A) data Tree = Leaf | Node Int Tree

(B) data Tree = Leaf | Node Tree Tree

(C) data Tree = Leaf | Node Int Tree Tree

(D) data Tree = Leaf Int | Node Tree Tree

(E) data Tree = Leaf Int | Node Int Tree Tree

data Tree = Leaf | Node Int Tree Tree

t1234 = Node 1 
          (Node 2 (Node 3 Leaf Leaf) Leaf) 
          (Node 4 Leaf Leaf)

Functions on trees

depth :: Tree -> Int
depth t = ??

QUIZ: Binary trees II

What is a Haskell datatype for binary trees with elements stored in the leaves?

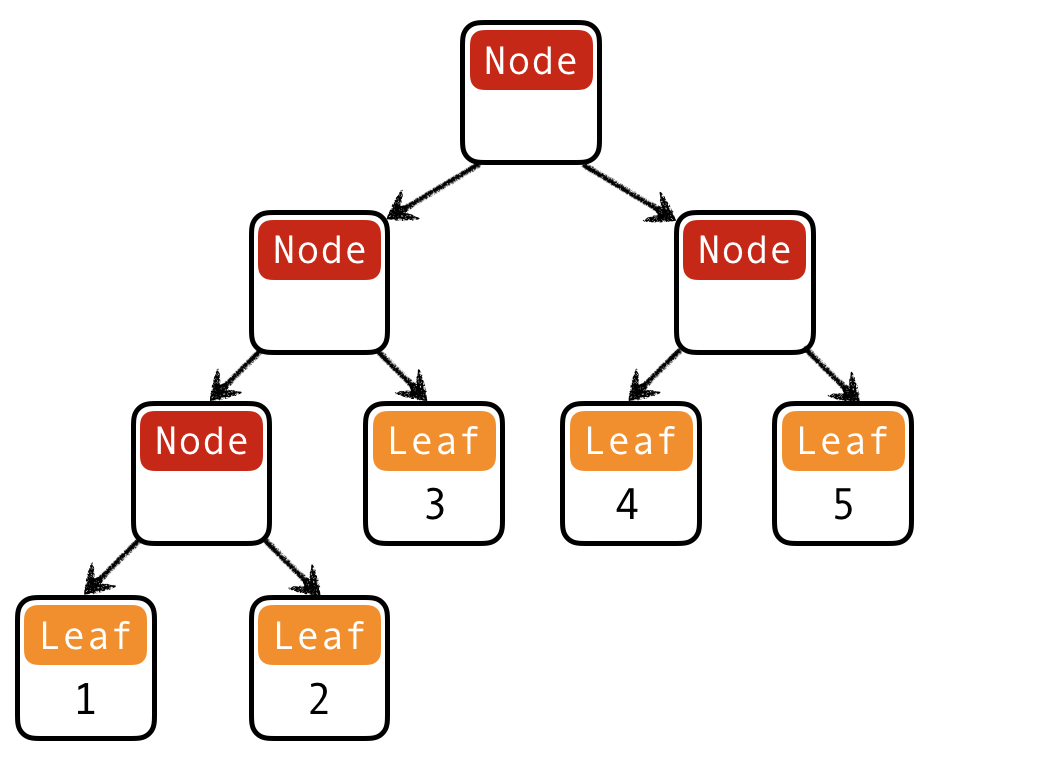
(A) data Tree = Leaf | Node Int Tree

(B) data Tree = Leaf | Node Tree Tree

(C) data Tree = Leaf | Node Int Tree Tree

(D) data Tree = Leaf Int | Node Tree Tree

(E) data Tree = Leaf Int | Node Int Tree Tree

data Tree = Leaf Int | Node Tree Tree

t12345 = Node
          (Node (Node (Leaf 1) (Leaf 2)) (Leaf 3))
          (Node (Leaf 4) (Leaf 5))

Why use Recursion?

1. Often far simpler and cleaner than loops

   • But not always…

2. Structure often forced by recursive data

3. Forces you to factor code into reusable units (recursive functions)

Why not use Recursion?

1. Slow

2. Can cause stack overflow

Example: factorial

fac :: Int -> Int
fac n
  | n <= 1    = 1
  | otherwise = n * fac (n - 1)

Lets see how fac 4 is evaluated:

<fac 4>
  ==> <4 * <fac 3>>              -- recursively call `fact 3`
  ==> <4 * <3 * <fac 2>>>        --   recursively call `fact 2`
  ==> <4 * <3 * <2 * <fac 1>>>>  --     recursively call `fact 1`
  ==> <4 * <3 * <2 * 1>>>        --     multiply 2 to result 
  ==> <4 * <3 * 2>>              --   multiply 3 to result
  ==> <4 * 6>                    -- multiply 4 to result
  ==> 24

Each function call <> allocates a frame on the call stack

• expensive
• the stack has a finite size

Can we do recursion without allocating stack frames?

Tail Recursion

Recursive call is the top-most sub-expression in the function body

• i.e. no computations allowed on recursively returned value

• i.e. value returned by the recursive call == value returned by function

QUIZ: Is this function tail recursive?

fac :: Int -> Int
fac n
  | n <= 1    = 1
  | otherwise = n * fac (n - 1)

A. Yes

B. No

Tail recursive factorial

Let’s write a tail-recursive factorial!

facTR :: Int -> Int
facTR n = ... 

HINT: Lets first write it with a loop

Lets see how facTR is evaluated:

<facTR 4>
  ==>    <<loop 1  4>> -- call loop 1 4
  ==>   <<<loop 4  3>>> -- rec call loop 4 3 
  ==>  <<<<loop 12 2>>>> -- rec call loop 12 2
  ==> <<<<<loop 24 1>>>>> -- rec call loop 24 1
  ==> 24                  -- return result 24! 

Each recursive call directly returns the result

• without further computation

• no need to remember what to do next!

• no need to store the “empty” stack frames!

Why care about Tail Recursion?

Because the compiler can transform it into a fast loop

facTR n = loop 1 n
  where
    loop acc n
      | n <= 1    = acc
      | otherwise = loop (acc * n) (n - 1)

function facTR(n){ 
  var acc = 1;
  while (true) {
    if (n <= 1) { return acc ; }
    else        { acc = acc * n; n = n - 1; }
  }
}

• Tail recursive calls can be optimized as a loop

  • no stack frames needed!

• Part of the language specification of most functional languages

  • compiler guarantees to optimize tail calls

That’s all folks!