Past three weeks
How to use essential language constructs?
- Data Types
- Recursion
- Higher-Order Functions
Next two weeks
How to implement language constructs?
Local variables and scope
Environments and Closures
(skip) Type Inference
Interpreter
How do we represent and evaluate a program?
Roadmap: The Nano Language
Features of Nano:
- Arithmetic
- Variables
- Let-bindings
- Functions
- Recursion
1. Nano: Arithmetic
A grammar of arithmetic expressions:
e ::= n
| e1 + e2
| e1 - e2
| e1 * e2| Expressions | Values | |
|---|---|---|
4 |
==> |
4 |
4 + 12 |
==> |
16 |
(4+12) - 5 |
==> |
11 |
Representing Arithmetic Expressions and Values

Lets represent arithmetic expressions as type
data Expr
= ENum Int -- ^ n
| EAdd Expr Expr -- ^ e1 + e2
| ESub Expr Expr -- ^ e1 - e2
| EMul Expr Expr -- ^ e1 * e2Lets represent arithmetic values as a type
type Value = Int
Evaluating Arithmetic Expressions

We can now write a Haskell function to evaluate an expression:
eval :: Expr -> Value
eval (ENum n) = n
eval (EAdd e1 e2) = eval e1 + eval e2
eval (ESub e1 e2) = eval e1 - eval e2
eval (EMul e1 e2) = eval e1 * eval e2
Alternative representation
Lets pull the operators into a separate type
data Binop = Add -- ^ `+`
| Sub -- ^ `-`
| Mul -- ^ `*`
data Expr = ENum Int -- ^ n
| EBin Binop Expr Expr -- ^ e1 `op` e2
QUIZ
Evaluator for alternative representation
eval :: Expr -> Value
eval (ENum n) = n
eval (EBin op e1 e2) = evalOp op (eval e1) (eval e2)What is a suitable type for evalOp?
{- 1 -} evalOp :: BinOp -> Value
{- 2 -} evalOp :: BinOp -> Value -> Value -> Value
{- 3 -} evalOp :: BinOp -> Expr -> Expr -> Value
{- 4 -} evalOp :: BinOp -> Expr -> Expr -> Expr
{- 5 -} evalOp :: BinOp -> Expr -> Value
The Nano Language
Features of Nano:
- Arithmetic [done]
- Variables
- Let-bindings
- Functions
- Recursion

2. Nano: Variables
Let’s add variables and let bindings!
e ::= n -- OLD
| e1 + e2
| e1 - e2
| e1 * e2
-- NEW
| x -- variablesLets extend our datatype
type Id = String
data Expr
= ENum Int -- OLD
| EBin Binop Expr Expr
-- NEW
| EVar Id -- variablesQUIZ
What should the following expression evaluate to?
x + 1(A) 0
(B) 1
(C) Error
Environment
An expression is evaluated in an environment
- A phone book which maps variables to values
[ "x" := 0, "y" := 12, ...]A type for environments
type Env = [(Id, Value)]
Evaluation in an Environment
We write
(eval env expr) ==> valueto mean
When expr is evaluated in environment env the result is value
So: when we have variables, we modify our evaluator (eval)
- to take an input environment
envin whichexprmust be evaluated.
eval :: Env -> Expr -> Value
eval env expr = -- ... value-of-expr-in-env...First, lets update the evaluator for the arithmetic cases ENum and EBin
eval :: Env -> Expr -> Value
eval env (ENum n) = ???
eval env (EBin op e1 e2) = ???
QUIZ
What is a suitable ?value such that
eval [ "x" := 0, "y" := 12, ...] (x + 1) ==> ?value(A) 0
(B) 1
(C) Error
QUIZ
What is a suitable env such that
eval env (x + 1) ==> 10(A) []
(B) [x := 0, y := 9]
(C) [x := 9, y := 0]
(D) [x := 9, y := 10, z := 666]
(E) [y := 10, z := 666, x := 9]
Evaluating Variables
Using the above intuition, lets update our evaluator to handle variables i.e. the EVar case:
eval env (EVar x) = ???
Lets confirm that our eval is ok!
envA = []
envB = ["x" := 0 , "y" := 9]
envC = ["x" := 9 , "y" := 0]
envD = ["x" := 9 , "y" := 10 , "z" := 666]
envE = ["y" := 10, "z" := 666, "x" := 9 ]
-- >>> eval envA (EBin Add (EVar "x") (ENum 1))
-- >>> eval envB (EBin Add (EVar "x") (ENum 1))
-- >>> eval envC (EBin Add (EVar "x") (ENum 1))
-- >>> eval envD (EBin Add (EVar "x") (ENum 1))
-- >>> eval envE (EBin Add (EVar "x") (ENum 1))
The Nano Language
Features of Nano:
- Arithmetic expressions [done]
- Variables [done]
- Let-bindings
- Functions
- Recursion

2. Nano: Variables
Let’s add variables and let bindings!
e ::= n -- OLD
| e1 + e2
| e1 - e2
| e1 * e2
| x
-- NEW
| let x = e1 in e2Lets extend our datatype
type Id = String
data Expr
= ENum Int -- OLD
| EBin Binop Expr Expr
| EVar Id
-- NEW
| ELet Id Expr ExprHow should we extend eval ?
QUIZ
What should the following expression evaluate to?
let x = 0
in
x + 1(A) Error
(B) 1
(C) 0
QUIZ
What should the following expression evaluate to?
let x = 0
in
let y = 100
in
x + y(A) Error
(B) 0
(C) 1
(D) 100
(E) 101
QUIZ
What should the following expression evaluate to?
let x = 0
in
let x = 100
in
x + 1(A) Error
(B) 0
(C) 1
(D) 100
(E) 101
QUIZ
What should the following expression evaluate to?
let x = 0
in
(let x = 100 in
in
x + 1
)
+
x(A) Error
(B) 1
(C) 101
(D) 102
(E) 2
Principle: Static/Lexical Scoping
Every variable use gets its value from a unique definition:
- “Nearest”
let-binder in program text
Static means you can tell without running the program
Great for readability and debugging
Define local variables
Be sure where each variable got its value
Don’t have to scratch head to figure where a variable got “assigned”
How to implement static scoping?
QUIZ
Lets re-evaluate the quizzes!
-- env
let x = 0
in -- ??? what env to use for `x + 1`?
x + 1(A) env
(B) [ ]
(C) [ ("x" := 0) ]
(D) ("x" := 0) : env
(E) env ++ ["x" := 0]
QUIZ
-- env
let x = 0
in -- (x := 0) : env
let y = 100
in -- ??? what env to use for `x + y` ?
x + y(A) ("x" := 0) : env
(B) ("y" := 100) : env
(C) ("y" := 100) : ("x" := 0) : env
(D) ("x" := 0) : ("y" := 100) : env
(E) [("y" := 100), ("x" := 0)]
QUIZ
Lets re-evaluate the quizzes!
-- env
let x = 0
in -- ("x" := 0) : env
let x = 100
in -- ??? what env to use for `x + 1`?
x + 1(A) ("x" := 0) : env
(B) ("x" := 100) : env
(C) ("x" := 100) : ("x" := 0) : env
(D) ("x" := 0) : ("x" := 100) : env
(E) [("x" := 100)]
Extending Environments
Lets fill in eval for the let x = e1 in e2 case!
eval env (ELet x e1 e2) = ???Evaluate
e1inenvto get a valuev1Extend environment with value for
xi.e. to(x := v1) : envEvaluate
e2using extended environment.
Lets make sure our tests pass!
Run-time Errors
Haskell function to evaluate an expression:
eval :: Env -> Expr -> Value
eval env (Num n) = n
eval env (Var x) = lookup x env -- (A)
eval env (Bin op e1 e2) = evalOp op v1 v2 -- (B)
where
v1 = eval env e1 -- (C)
v2 = eval env e2 -- (C)
eval env (Let x e1 e2) = eval env1 e2
where
v1 = eval env e1
env1 = (x, v1) : env -- (D)QUIZ
Will eval env expr always return a value ? Or, can it crash?
(A) operation at A may fail (B) operation at B may fail (C) operation at C may fail (D) operation at D may fail (E) nah, its all good…, always returns a Value
Free vs bound variables
Undefined Variables
How do we make sure lookup doesn’t cause a run-time error?
Bound Variables
Consider an expression let x = e1 in e2
An occurrence of
xis bound ine2i.e. when occurrence of form
let x = ... in ... x ...i.e. when
xoccurs “under” aletbinding forx.
Free Variables
An occurrence of x is free in e if it is not bound in e
Closed Expressions
An expression e is closed in environment env:
- If all free variables of
eare defined inenv
Successful Evaluation
lookup will never fail
- If
eval env eis only called onethat is closed inenv
QUIZ
Which variables occur free in the expression?
let y = (let x = 2
in x ) + x
in
let x = 3
in
x + y(A) None
(B) x
(C) y
(D) x and y
Exercise to try at home
Consider the function
evaluate :: Expr -> Value
evaluate e
| isOk e = eval emptyEnv e
| otherwise = error "Sorry! bad expression, it will crash `eval`!"
where
emptyEnv = [] -- has NO bindingsWhat should isOk check for? (Try to implement it for nano…)
The Nano Language
Features of Nano:
- Arithmetic expressions [done]
- Variables [done]
- Let-bindings [done]
- Functions
- Recursion

Nano: Functions
Let’s add
lambda abstraction (aka function definitions)
application (aka function calls)
e ::= n -- OLD
| e1 `op` e2
| x
| let x = e1 in e2
-- NEW
| \x -> e -- abstraction
| e1 e2 -- applicationExample
let incr = \x -> x + 1
in
incr 10
Representation
data Expr
= ENum Int -- OLD
| EBin Binop Expr Expr
| EVar Id
| ELet Id Expr Expr
-- NEW
| ??? -- abstraction \x -> e
| ??? -- application (e1 e2)
Representation
data Expr
= ENum Int -- OLD
| EBin Binop Expr Expr
| EVar Id
| ELet Id Expr Expr
-- NEW
| ELam Id Expr -- abstraction \x -> e
| EApp Expr Expr -- application (e1 e2)Example
let incr = \x -> x + 1
in
incr 10is represented as
ELet "incr" (ELam "x" (EBin Add (EVar "x") (ENum 1)))
(
EApp (EVar "incr") (ENum 10)
)
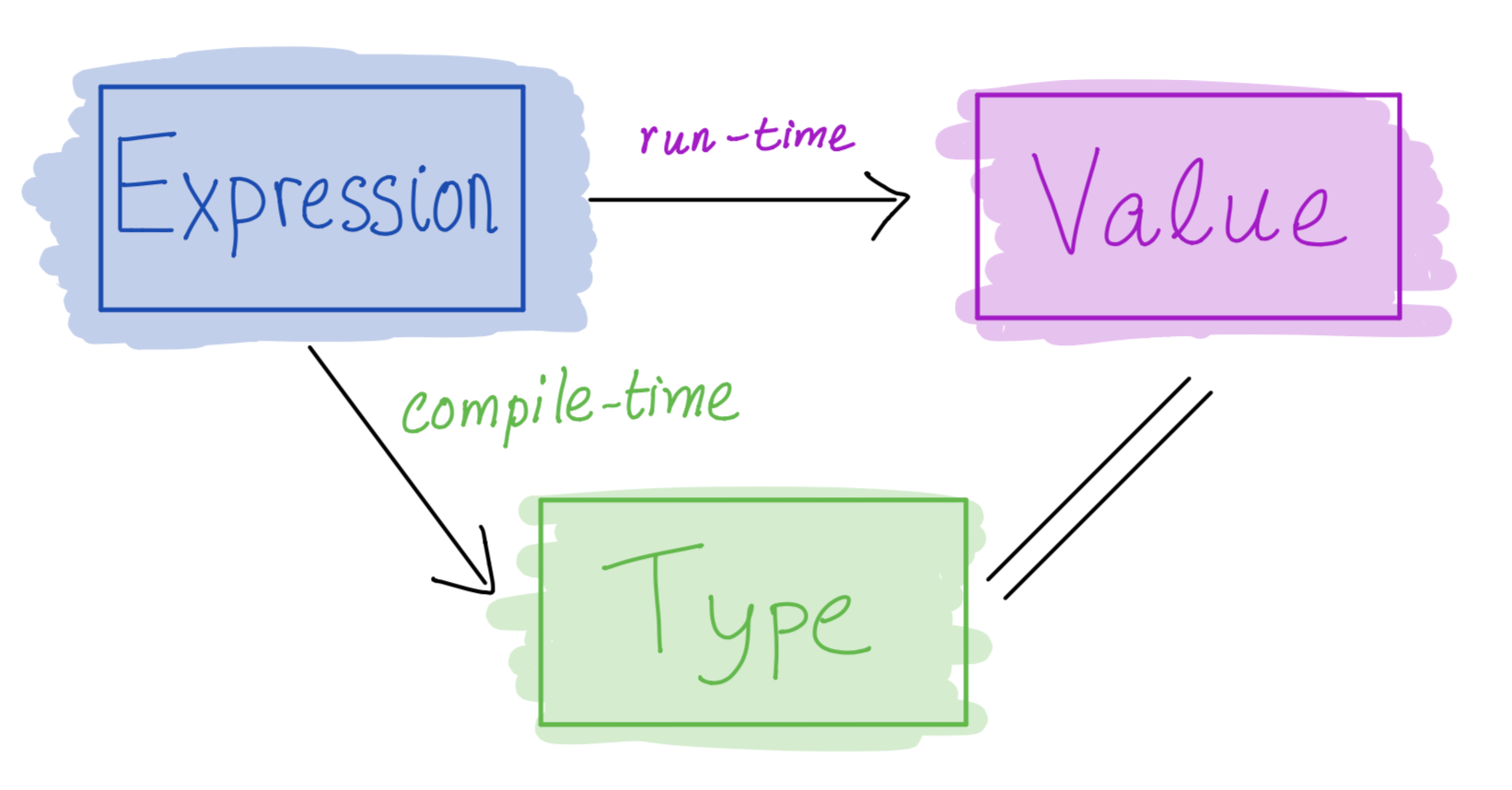
Functions are Values
Recall the trinity

But… what is the value of a function?
Lets build some intuition with examples.
QUIZ
What does the following expression evaluate to?
let incr = \x -> x + 1 -- abstraction ("definition")
in
incr 10 -- application ("call")(A) Error/Undefined
(B) 10
(C) 11
(D) 0
(E) 1
What is the Value of incr?
Is it an
Int?Is it a
Bool?Is it a ???
What information do we need to store (in the Env) about incr?
A Function’s Value is its Code
-- env
let incr = \x -> x + 1
in -- ("incr" := <code>) : env
incr 10 -- evaluate <code> with parameter := 10What information do we store about <code> ?
A Call’s Value
How to evaluate the “call” incr 10 ?
Lookup the
<code>i.e.<param, body>forincr(stored in the environment),Evaluate
bodywithparamset to10!
Two kinds of Values
We now have two kinds of Values
v ::= n -- OLD
| <x, e> -- <param, body>- Plain
Int(as before) - A function’s “code”: a pair of “parameter” and “body-expression”
data Value
= VInt Int -- OLD
| VCode Id Expr -- <x, e>
Evaluating Lambdas and Applications
eval :: Env -> Expr -> Value
-- OLD
eval env (ENum n) = ???
eval env (EVar x) = ???
eval env (EBin op e1 e2) = ???
eval env (ELet x e1 e2) = ???
-- NEW
eval env (ELam x e) = ???
eval env (EApp e1 e2) = ???Lets make sure our tests work properly!
exLam1 = ELet "incr" (ELam "x" (EBin Add (EVar "x") (ENum 1)))
(
EApp (EVar "incr") (ENum 10)
)
-- >>> eval [] exLam1
-- 11QUIZ
What should the following evaluate to?
let c = 1
in
let inc = \x -> x + c
in
inc 10(A) Error/Undefined
(B) 10
(C) 11
(D) 0
(E) 1
exLam2 = ELet "c" (ENum 1)
(ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
(
EApp (EVar "incr") (ENum 10)
)
)
-- >>> eval [] exLam2
-- ???QUIZ
And what should this expression evaluate to?
let c = 1
in
let inc = \x -> x + c
in
let c = 100
in
inc 10(A) Error/Undefined
(B) 110
(C) 11
The “Immutability Principle”
A function’s behavior should never change
- A function must always return the same output for a given input
Why?
> myFunc 10
0
> myFunc 10
10Oh no! How to find the bug? Is it
- In
myFuncor - In a global variable or
- In a library somewhere else or
- …
My worst debugging nightmare
Colbert “Immutability Principle”
The Immutability Principle ?
How does our eval work?
exLam3 = ELet "c" (ENum 1)
(
ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
(
ELet "c" (ENum 100)
(
EApp (EVar "incr") (ENum 10)
)
)
)
-- >>> eval [] exLam3
-- ???Oops?
-- []
let c = 1
in -- ["c" := 1]
let inc = \x -> x + c
in -- ["inc" := <x, x+c>, c := 1]
let c = 100
in -- ["c" := 100, "inc" := <x, x+c", "c" := 1] <<< env
inc 10And so we get
eval env (inc 10)
==> eval ("x" := 10 : env) (x + c)
==> 10 + 100
==> 110Ouch.
Enforcing Immutability with Closures
How to enforce immutability principle
inc 10always returns11?
Key Idea: Closures
At definition: Freeze the environment the function’s value
At call: Use the frozen environment to evaluate the body
Ensures that inc 10 always evaluates to the same result!
-- []
let c = 1
in -- ["c" := 1]
let inc = \x -> x + c
in -- ["inc" := <frozenv, x, x+c>, c := 1] <<< frozenv = ["c" := 1]
let c = 100
in -- ["c" := 100, "inc" := <frozenv, x, x+c>, "c" := 1]
inc 10Now we evaluate
eval env (inc 10)
==> eval ("x" := 10 : frozenv) (x + c) where frozenv = ["c" := 1]
==> 10 + 1
==> 1tada!
Representing Closures
Lets change the Value datatype to also store an Env
data Value
= VInt Int -- OLD
| VClos Env Id Expr -- <frozenv, param, body>
Evaluating Function Definitions
How should we fix the definition of eval for ELam?
eval :: Env -> Expr -> Value
eval env (ELam x e) = ???Hint: What value should we bind incr to in our example above?
(Recall At definition freeze the environment the function’s value)
Evaluating Function Calls
How should we fix the definition of eval for EApp?
eval :: Env -> Expr -> Value
eval env (EApp e1 e2) = ???(Recall At call: Use the frozen environment to evaluate the body)
Hint: What value should we evaluate incr 10 to?
- Evaluate
incrto get<frozenv, "x", x + c> - Evaluate
10to get10 - Evaluate
x + cinx:=10 : frozenv
Let’s generalize that recipe!
- Evaluate
e1to get<frozenv, param, body> - Evaluate
e2to getv2 - Evaluate
bodyinparam := v2 : frozenv
Immutability Achieved
Lets put our code to the test!
exLam3 = ELet "c" (ENum 1)
(
ELet "incr" (ELam "x" (EBin Add (EVar "x") (EVar "c")))
(
ELet "c" (ENum 100)
(
EApp (EVar "incr") (ENum 10)
)
)
)
-- >>> eval [] exLam3
-- ???
QUIZ
What should the following evaluate to?
let add = \x -> (\y -> x + y)
in
let add10 = add 10
in
let add20 = add 20
in
(add10 100) + (add20 1000)A. 1100
B. 1110
C. 1120
D. 1130
E. 1140
Functions Returning Functions Achieved!
exLam4 = ...
-- >>> eval [] exLam4
Practice
What should the following evaluate to?
let add = \x -> (\y -> x + y)
in
let add10 = add 10
in
let doTwice = \f -> (\x -> f (f x))
in
doTwice add10 100
Functions Accepting Functions Achieved!
exLam5 = ...
-- >>> eval [] exLam4
The Nano Language

Features of Nano:
- Arithmetic expressions [done]
- Variables [done]
- Let-bindings [done]
- Functions [done]
- Recursion
… You figure it out Hw4 … :-)
