News

HW 5 is out, due Sun 6/11

Logic Programming

Traditional Languages

Program = Algorithm + Data Structures
Execute

Prolog

Program = Facts + Rules
Query

Logic Programming

Prolog History

1970s: Logic + Automated Theorem Proving
Developed for Artificial Intelligence

Prolog : Original Vision “Expert Systems”

Collection of Facts

Carnitas is Mexican isMexican(carnitas)

Collection of Rules

Mexican food is delicious if isMexican(X) then isDelicious(X)

Queries

What is a delicious food ? hey! solve for Y. s.t. isDelicious(Y)

Deductions

Carnitas!

You don’t RUN Prolog, you ASK it QUESTIONS

Declarative Programming

Specify what you want
Specify desired properties of result
Not how to obtain result

Declarative: Ideal for SEARCHING For Results

Declarative Programming

Ideal for Searching Large Space of Results

Philosophy

It is often hard to specify search algorithm
But easy to specify the characteristics of the solution.

Declarative Programming Examples…

Declarative Programming: Orbitz/Expedia/etc.

Collection of Facts

Airports, Flights, Times, Durations, Costs

Collection of Rules

If travel from A to B with price (P1) AND B to C with price (P2)…

Then

travel from A to C with price (P1 + P2) …

Queries

What is cheapest flight from SAN to JFK with duration < 6 Hrs ?

Declarative Programming: Linear Programming

Collection of Facts

El Cuervo makes CA Burrito (profit = $2), Fish Taco (profit = $1)

Collection of Rules

Burrito Capacity < 200
Taco Capacity < 400
Total Capacity < 300

Query: How many burritos and tacos to maximize profit?

max     2.burr + 1.taco       /* profit           */
s.t.    burr      <  200      /* burrito capacity */
        taco      < 400       /* taco    capacity */
        burr+taco < 300       /* total   capacity */
        0        <= burr
        0        <= taco      /* must produce!    */

Declarative Programming

Used heavily in many domains (together with statistical methods)

Scheduling
Travel, Sports, …
Rule-based Anomaly detection
Credit card fraud!
SQL (and similar DB Query Languages)
Find all pairs of stocks, with same price on same day,
More than 50 times last year
Many of these are inspired-by / subsets of Prolog …

Prolog: New Way To Think About Programming …

Prolog: … Programming As Proving!

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Language: Terms

Prolog Program

Facts
Rules

… but facts and rules about what ?

Terms

Terms are Prolog’s way of representing Data

“Tree-like” values, similar to Ocaml ADTs

Four Kinds of Terms

Constants
Atoms
Variables
Compound Terms

Prolog Terms: Constants

Constants the simplest term, representing primitive values

Basic types like integers, reals
Examples: 1, 92, 4.4

Prolog Terms: Atoms

Atom: any identifier starting with lower-case

x, alice, taco, giraffe, appleSauce

Atoms are NOT variables

Prolog Terms: Atoms

Atom: any identifier starting with lower-case

x, alice, taco, giraffe, appleSauce

Atoms are not variables

Elements of a single mega enum type
Similar to tags used in ML types (except ML tags are uppercase)
type atoms = x | alice | taco | giraffe | appleSauce | ...

Prolog Terms: Atoms

Atom: any identifier starting with lower-case

x, alice, taco, giraffe, appleSauce

Atoms are Uninterpreted Constants (Names)

Prolog knows NOTHING about the tags, they are just names
Each tag is equal to itself (more later…)
alice = alice
taco = taco
Each tag is disequal to every other tag
alice = taco never holds in Prolog

Prolog Terms: Variables

Variables: any identifier starting with upper-case

X, Y, Z, Head, Tail, Taco, Burrito, Alice, Bob
_ is the wildcard variable, similar to ML

Variables are quite special …

Even though x = a makes no sense to Prolog …
… X = a does have a meaning but not what you might think!

Warning: Upper vs. Lowercase leads to errors

Prolog Terms: Compound Terms

Compound terms are of form atom(term1, term2, term3, ...)

Where each term is one-of

constant
atom
variable
compound term

Prolog Terms: Compound Terms

Compound terms are of form atom(term1, term2, term3, ...)

Where each term is one-of

constant
atom
variable
compound term

Examples

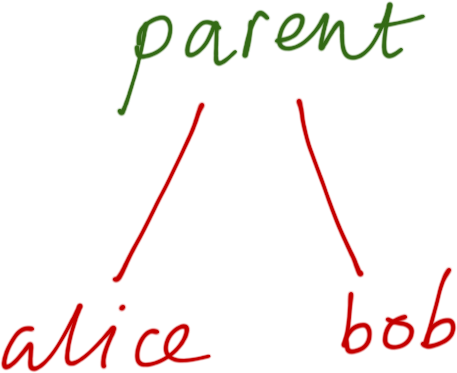
x(y, z)              % y, z       are atoms
parent(alice, bob)   % alice, bob are atoms
parent(alice, Child) % alice is an atom, Child is a variable

Prolog Terms ARE NOT function calls

Prolog Compound Terms

Terms are NOT Function Calls!
More like trees

Prolog Terms: Compound Terms

Compound terms are of form atom(term1, term2, term3, ...)

Each term is one-of

constant
atom
variable
compound term

An Ocaml Type For Prolog Terms

type term
  = Constant of int
  | Atom     of string
  | Variable of string
  | Compound of string * term list

QUIZ: An Ocaml Type For Prolog Terms

type term
  = Constant of int
  | Atom     of string
  | Variable of string
  | Compound of string * term list

(Hint: atom = lowercase, variable = uppercase)

Which Ocaml value of type term represents Prolog term

parent(alice, bob) ?

A. parent ("alice", "bob")

B. parent (Atom "alice", Atom "bob")

C. [Atom "parent"; Atom "alice"; Atom "bob"]

D. Compound ("parent", [Atom "alice"; Atom "bob"])

E. Compound (Atom "parent", [Atom "alice"; Atom "bob"])

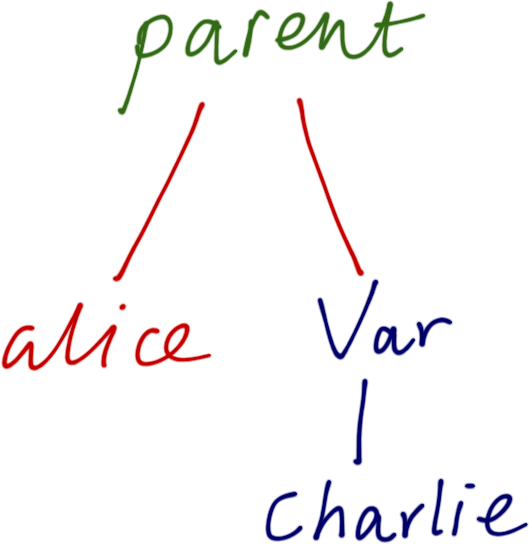
Prolog Compound Terms

Prolog term parent(alice, Charlie) is represented by:

Ocaml Value

Compound ("parent", [Atom "alice"; Var "Charlie"])

Tree

QUIZ: An Ocaml Type For Prolog Terms

type term
  = Constant of int
  | Atom     of string
  | Variable of string
  | Compound of string * term list

(Hint: atom = lowercase, variable = uppercase)

What Ocaml value of type term represents Prolog term factorial(5) ?

A. factorial(5)

B. factorial(Atom 5)

C. 120

D. Constant 120

E. Compound ("factorial", [Constant 5])

Prolog Terms

Prolog term factorial(5) is simply the tree

The term is just a box containing 5 labeled factorial

Function Symbols

factorial just a label called a function symbol
Prolog has no idea about implementation of function …

Prolog Terms = (Tree) Structured Data

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Language: Facts

Example

The following facts specify a list of parent-child relationships

parent(kim, holly).  
parent(margaret, kim).  
parent(herbert, margaret).
parent(john, kim).
parent(felix, john).  
parent(albert, felix).

Note kim, holly, margaret etc. are all atoms
Facts are just terms (typically without variables.)
Specified by term followed by .

Prolog maintains a Database of facts

You can make up and add new facts to the collection
We will be able to ask Prolog queries over these facts

Predicates = Function Symbols Used For Facts

Represent functions that evaluate to a boolean
e.g. parent is a predicate of arity 2 (that takes 2 arguments)

Predicates Are Just Names: No Meaning Or Implementation

parent is a predicate of arity 2 (that takes two arguments)
Programmer mentally notes that:
- parent(kim, holly) means kim is a “parent-of” holly
- parent(margaret, kim) means margaret is a “parent-of” kim
- etc.

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Running Prolog via Queries

Language: Queries

Standard interface is a REPL shell

$ rlwrap swipl

130f@ieng6-202]:~:501$ swipl
Welcome to SWI-Prolog (Multi-threaded, 32 bits, Version 5.10.5)
Copyright (c) 1990-2011 University of Amsterdam, VU Amsterdam
SWI-Prolog comes with ABSOLUTELY NO WARRANTY. This is free software,
and you are welcome to redistribute it under certain conditions.
Please visit http://www.swi-prolog.org for details.

For help, use ?- help(Topic). or ?- apropos(Word).

?-

Language: Queries

Suppose we have a collection of facts saved in lec-prolog.pl

You can load the facts in …

?- consult('lec-prolog.pl').
% foo.pl compiled 0.00 sec, 10,640 bytes
true.

… or you can add them one-at-a-time

?- assert(parent(margaret, kim)).

Language: Queries

Once facts are loaded, you query Prolog as follows:

Plg: Prompts you to type a query
You: Type a query
Plg: Tries to prove your query
Plg: Prints out the result (or failure)
Repeat (go to 1)

Lets ask some questions!

Language: Queries

The simplest possible query …

?- parent(margaret, john).

… a fact but typed at the prompt.

Language: Queries

The simplest possible query …

?- parent(margaret, john).

… a fact but typed at the prompt.

Meaning

O Prolog, is this fact in your Database … or can it be inferred from your database?

Language: Queries

The simplest possible query …

?- parent(margaret, john).

… a fact but typed at the prompt.

Meaning

O Prolog, is this fact in your database … or can it be inferred from your database?

Prolog Replies

?- parent(margaret, john).
false.

This is not one of the facts we gave it, and,
We are yet to supply it with rules for inferring new facts.

Language: Queries

A slightly different query yields a different result.

Language: Queries

A slightly different query yields a different result.

?- parent(margaret, kim).  
true.

As this was indeed one of the facts loaded in lec-prolog

Pfft. Big deal? Is Prolog just a table lookup?!

Things get more interesting when queries have variables …

Queries With Variables

This is where Prolog starts to depart radically from other paradigms…

?- parent(margaret, X).

Meaning

O Prolog, for which value(s) of X is the fact provable ?

Queries With Variables

This is where Prolog starts to depart radically from other paradigms…

?- parent(margaret, X).

Meaning

O Prolog, for which value(s) of X is the fact provable ?

Prolog Replies

X = kim.

As when prolog plugs-in kim for X,

It can infer parent(margaret, kim).

Queries With Variables

Suppose we flip the query.

?- parent(X, kim).

O Prolog, for which value(s) of X is parent(X, kim) provable ?

Queries With Variables

Suppose we flip the query.

?- parent(X, kim).

O Prolog, who are the parents-of kim?

Queries With Variables

Suppose we flip the query.

?- parent(X, kim).

O Prolog, who are the parents-of kim?

Prolog Replies

?- parent(X, kim).
X = margaret ; % [press ';' if you want another solution]
X = john ;     % [press ';' if you want another solution]
false.         % [thats all folks, no more solutions    ]

Returns all solutions for X that make parent(X, kim) provable.

Queries With Variables

We can write queries with multiple variables.

?- parent(X, Y).

O Prolog, for which pairs X, Y is parent(X, Y) provable?

Queries With Variables

We can write queries with multiple variables.

?- parent(X, Y).

O Prolog, for which pairs X, Y is parent(X, Y) provable?

Prolog Replies

?- parent(X, Y).
X = kim,      Y = holly   ;
X = margaret, Y = kim     ;
X = herbert,  Y = margaret;
X = john,     Y = kim     ;
X = felix,    Y = john    ;
X = albert,   Y = felix   ;
X = albert,   Y = dana    ;
X = felix,    Y = maya    .

Enumerates all facts in the parent database.

QUIZ: Queries With Variables

Suppose we want to know if there are any strange circularities in the database:

Does there exist any person who is their own parent ?

Which of the following encodes the above in Prolog?

A. parent(kim, kim)

B. parent(x, x)

C. parent(X, X)

D. parent(X, Y)

E. parent(Y, X)

Queries are magic!

Queries Work Like Magic

In Java/C# or for that matter ML/Scala/… you would need

Some parentOf or childOf methods
- to represent parent-child relationship
Some looping or iteration
- to search through all pairs
Instead, Prolog uses facts and queries
- to search forwards and backwards
- to enumerate all results
- in a single uniform declarative manner!

Magic = Unification + Backtracking Search

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Unification: Prolog’s computational heart

Unification: When does one term MATCH another?

Unification

Two Terms Can Be Unified If

We can substitute values for their variables to make the terms identical

Unification

Two terms can be unified if we can substitute values for variables to make the terms identical

Equality Is Unification

In Prolog, when you write (e.g. in a query)

?- term1 = term2.

you are asking whether term1 can be unified with term2.

Unification By Example

Unification: Atoms

Two terms can be unified if we can substitute values for variables to make the terms identical

Example

?- kim = kim.
true.

Two same atoms are trivially unified.

Unification: Atoms

Two terms can be unified if we can substitute values for variables to make the terms identical

Example

?- kim = holly.
false.

Two different atoms can never be unified.

Unification: Compound Terms Are Recursively Unified

Two terms can be unified if we can substitute values for variables to make the terms identical

Example

?- foo(kim) = foo(kim).
true.

As there are no variables, and the terms are already identical.

Example

?- foo(kim) = foo(holly).
false.

As there are no variables, and the terms can never be identical.

Unification: Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

Example

?- X = kim.

Q: When is the term X identical to the term kim?
A: When we substitute X with the value kim!

Unification: Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

Example

?- foo(X) = foo(kim).

Q: When is the term X identical to the term kim?
A: When we substitute X with the value kim!

Prolog Responds

?- foo(X) = foo(kim).
X = kim.

Pretty simple…

QUIZ: Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following query?

?- foo(X, dog) = foo(cat, Y).

A. false

B. X = cat, Y = cat.

C. X = dog, Y = dog.

D. X = dog, Y = cat.

E. X = cat, Y = dog.

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).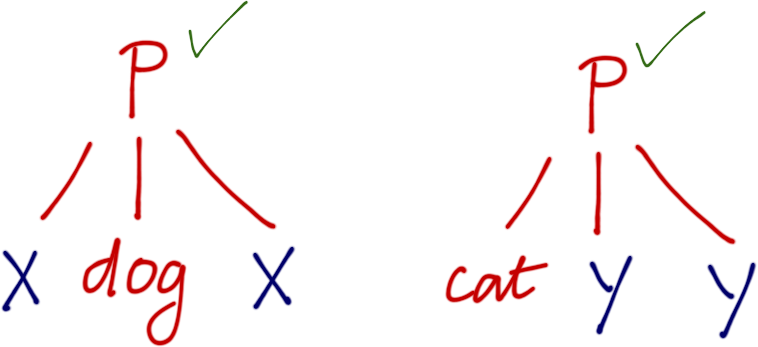

The top nodes of both trees have same predicate … go inside.

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).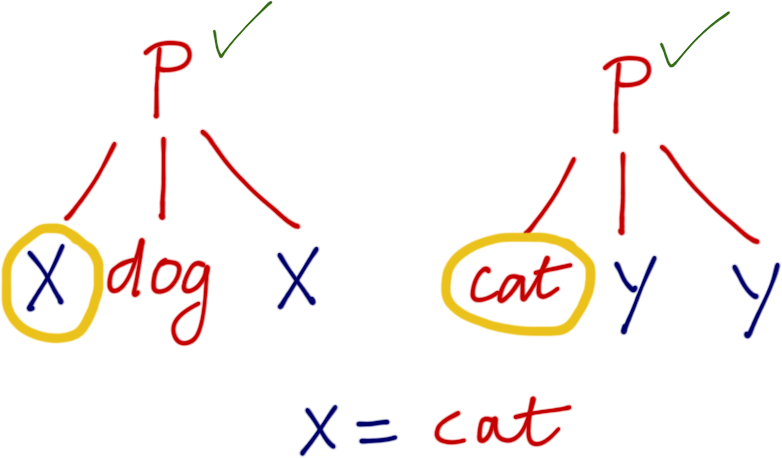

To unify X and cat use substitution X = cat

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).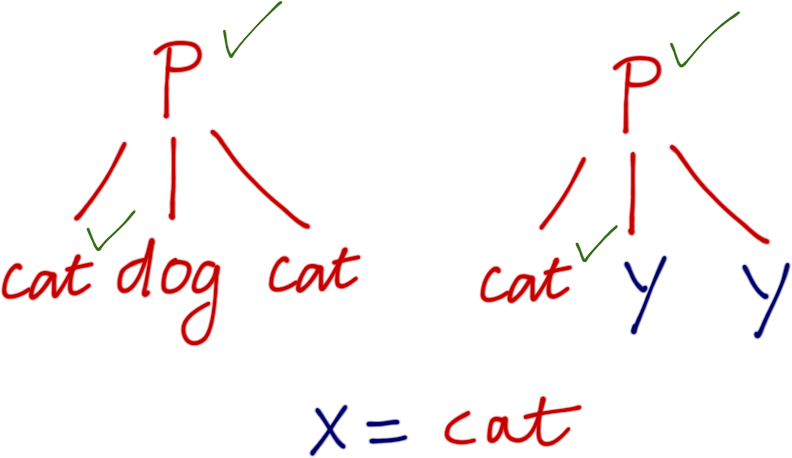

Apply substitution X = cat to both terms. Move on to next leaf…

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).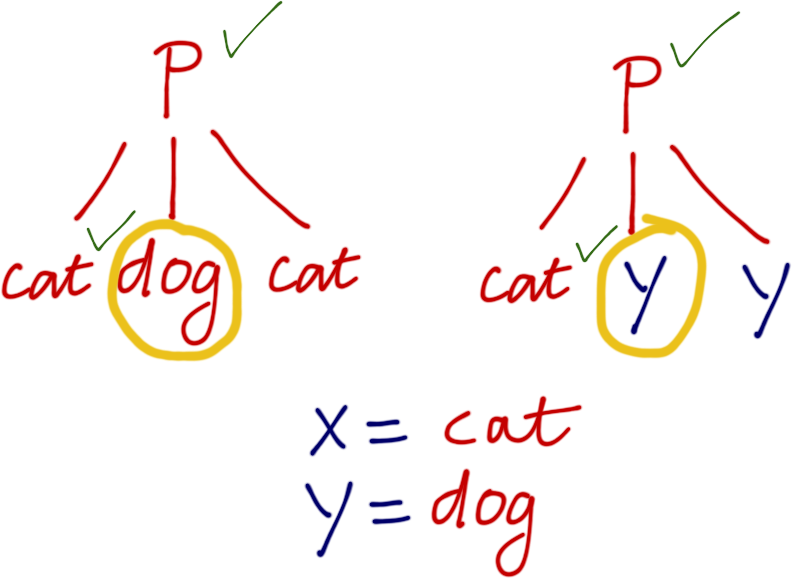

To unify dog and Y use substitution Y = dog …

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).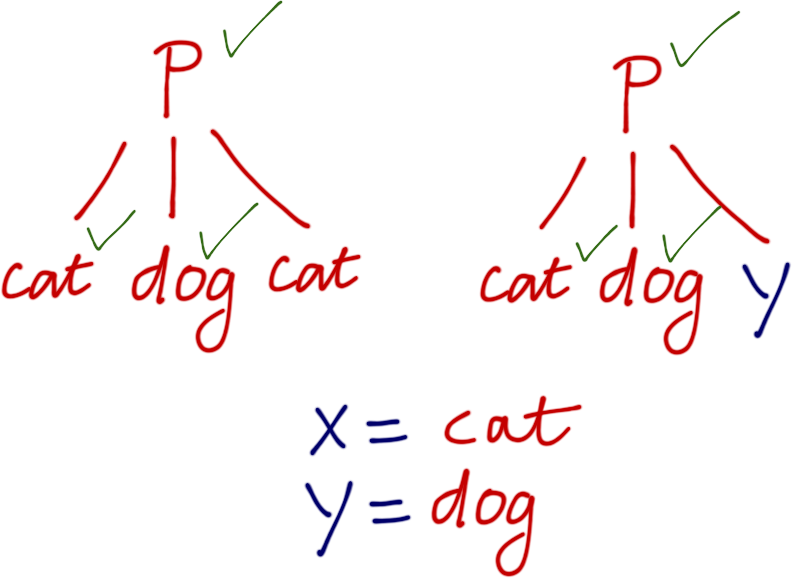

… and apply substitution throughout both terms.

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).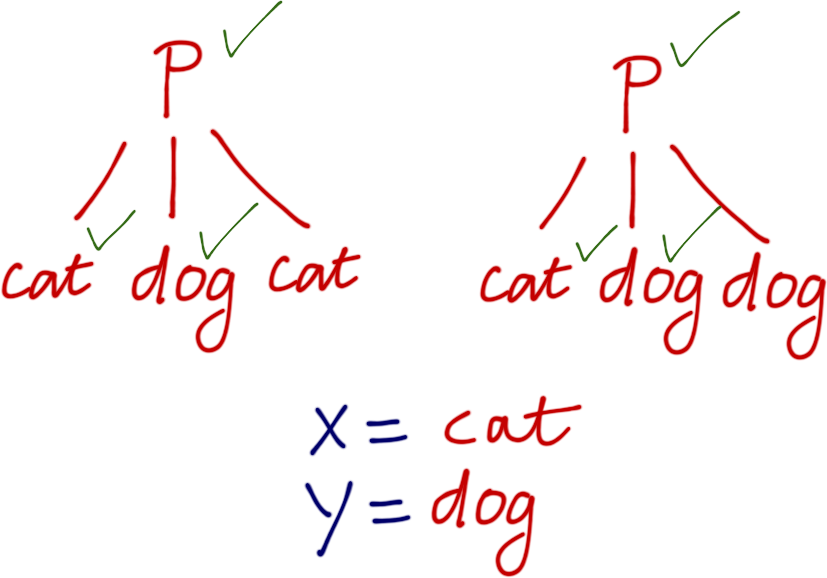

Uh oh, now last leaf has different atoms…

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).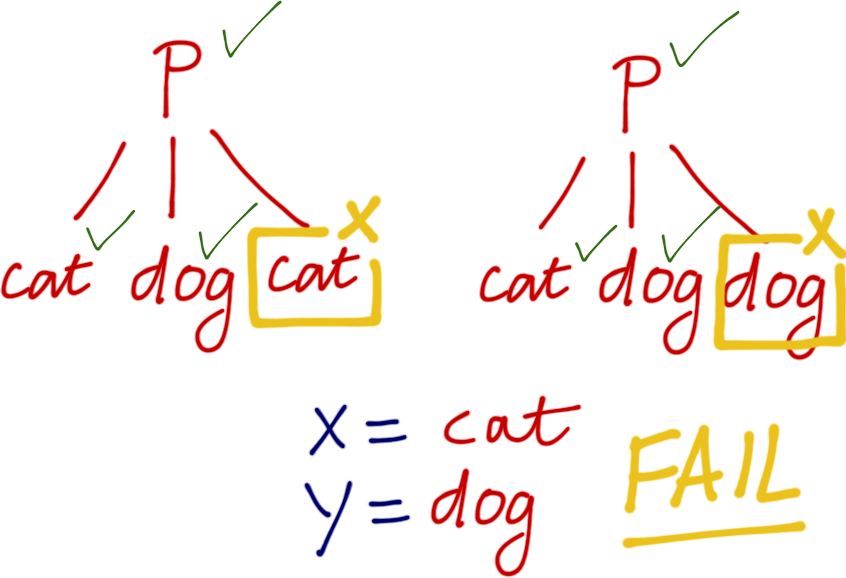

… impossible to unify cat and dog. Unification fails.

Unification With Multiple Variables

Two terms can be unified if we can substitute values for variables to make the terms identical

?- p(X, dog, X) = p(cat, Y, Y).
false.

QUIZ: Recursively Unify Subtrees

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following unification query?

?- a(W, foo(W, Y), Y) = a(2, foo(X, 3), Z).

A. false. (No unification possible)

B. W = 2, X = 2, Y = 2, Z = 2.

C. W = 2, X = 2, Y = 3, Z = 3.

D. W = 3, X = 3, Y = 2, Z = 2.

C. W = 2, X = 3, Y = 2, Z = 3.

Recursively Unify Subtrees

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following unification query?

?- a(W, foo(W, Y), Y) = a(2, foo(X, 3), Z).

Subst W = 2. Query is: a(2, foo(2, Y), Y) = a(2, foo(X, 3), Z).
Subst X = 2. Query is: a(2, foo(2, Y), Y) = a(2, foo(2, 3), Z).
Subst Y = 3. Query is: a(2, foo(2, 3), 3) = a(2, foo(2, 3), Z).
Subst Z = 3. Query is: a(2, foo(2, 3), 3) = a(2, foo(2, 3), 3).
Done!

Recursively Unify Subtrees

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following unification query?

?- a(W, foo(W, Y), Y) = a(2, foo(X, 3), Z).
W = 2,
X = 2,
Y = 3,
Z = 3.

QUIZ: Recursively Unify Subtrees

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following unification query?

?- a(W, foo(W, Y), Y) = a(2, foo(X, 3), X).

A. false. (No unification possible)

B. W = 2, X = 2, Y = 2, Z = 2.

C. W = 2, X = 2, Y = 3, Z = 3.

D. W = 3, X = 3, Y = 2, Z = 2.

E. W = 2, X = 3, Y = 2, Z = 3.

Recursively Unify Subtrees

Two terms can be unified if we can substitute values for variables to make the terms identical

How does Prolog respond to the following unification query?

?- a(W, foo(W, Y), Y) = a(2, foo(X, 3), X).

Subst W = 2. Query is: a(2, foo(2, Y), Y) = a(2, foo(X, 3), X).
Subst X = 2. Query is: a(2, foo(2, Y), Y) = a(2, foo(2, 3), 2).
Subst Y = 3. Query is: a(2, foo(2, 3), 3) = a(2, foo(2, 3), 2).
3 = 2 cannot be unified, Fail!

Unification: Powerful Way To Answer Queries

Unification is a Powerful Way To Answer Queries

When we ask

?- parent(margaret, X).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds then it replies true
- And also the unifying substitutions for X
- Which are the solutions for the query!
If unification fails then it replies false

Unification is a Powerful Way To Answer Queries

When we ask

?- parent(margaret, X).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds then it replies true (and the solutions for X)
If unification fails then it replies false

Above Query Has One Solution

?- parent(margaret, X).  
X = kim.

Unification is a Powerful Way To Answer Queries

When we ask

?- parent(X, kim).

Unification is a Powerful Way To Answer Queries

When we ask

?- parent(X, kim).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds then it replies true (and the solutions for X)
If unification fails then it replies false

Unification is a Powerful Way To Answer Queries

When we ask

?- parent(X, kim).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds then it replies true (and the solutions for X)
If unification fails then it replies false

This Query Has Many Solutions

?- parent(X, kim).  
X = margaret ;
X = john     .

Unification is a Powerful Way To Answer Queries

Finally, when we ask

?- parent(X, Y).

Unification is a Powerful Way To Answer Queries

Finally, when we ask

?- parent(X, Y).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds it replies true (and solutions for X, Y)
If unification fails it replies false

Unification is a Powerful Way To Answer Queries

Finally, when we ask

?- parent(X, Y).

Prolog checks if the above term can be unified with any known fact (term).

If unification succeeds it replies true (and solutions for X, Y)

This Query Has Many Solutions: All known facts

?- parent(X, Y).
X = kim,      Y = holly   ;
X = margaret, Y = kim     ;
X = herbert,  Y = margaret;
X = john,     Y = kim     ;
X = felix,    Y = john    ;
X = albert,   Y = felix   ;
X = albert,   Y = dana    ;
X = felix,    Y = maya    .

Unification Lets Prolog Answer Queries Magically!

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Rules

Digression: Conjunctions, Queries about MANY terms

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to determine if margaret is the grandparent of holly

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to determine if margaret is the grandparent of holly

?- parent(margaret, X), parent(X, holly).

Is there a person X who is a child of margaret AND a parent of holly ?
Is there X s.t. parent(margaret, X) AND parent(X, holly) ?

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to determine if margaret is the grandparent of holly

?- parent(margaret, X), parent(X, holly).

Is there a person X who is a child of margaret AND a parent of holly ?
Is there X s.t. parent(margaret, X) AND parent(X, holly) ?

Apparently

?- parent(margaret, X), parent(X, holly).
X = kim.

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to find the great-grandparents of kim

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to find the great-grandparents of kim

?- parent(GGP, GP), parent(GP, P), parent(P, kim).

Note: how we link the terms with a variable to capture relationships.

Conjunction: Comma-separated Sequence of terms

Often useful to ask questions over multiple terms.

For example, to find the great-grandparents of kim

?- parent(GGP, GP), parent(GP, P), parent(P, kim).

Note: how we link the terms with a variable to capture relationships.

Prolog finds appropriate unifiers and replies

?- parent(margaret, X), parent(X, holly).
GGP = john,
GP  = felix,
P   = albert.

i.e. john is a great-grandparent following the above chain.

QUIZ: Conjunctions

Which of these queries is true iff margaret and kim are (half-) siblings?

A. parent(margaret, kim)

B. parent(margaret, X), parent(X, kim).

C. parent(kim, X), parent(X, margaret).

D. parent(margaret, X), parent(kim, X).

E. parent(X, margaret), parent(X, kim).

Recap: Conjunctions

Conjunctions let us mine the database for complex relationships…
… but its cumbersome to repeatedly write down long queries
We need a way to compose complex queries from simple queries…

Rules

Rules: Complex Predicates from Simple Queries

Format

headQuery :- condQuery1, condQuery2, condQuery3,...

Rules: Complex Predicates from Simple Queries

Format

headQuery :- condQuery1, condQuery2, condQuery3,...

Intuition 1 (Forwards)

If you can prove condQuery1 AND condQuery2 AND ...
Then you can prove headQuery

Rules: Complex Predicates from Simple Queries

Format

headQuery :- condQuery1, condQuery2, condQuery3,...

Intuition 2 (Backwards)

To prove the goal headQuery …
Prove subgoals condQuery1 AND condQuery2 AND …

Rules: Complex Predicates from Simple Queries

An Example: Defining a `grandparent` predicate

Our database includes a parent predicate
Let us use it to define a grandparent predicate

Rules: Complex Predicates from Simple Queries

An Example: Defining a `grandparent` predicate

grandparent(GP, GC) :- parent(GP, P), parent(P, GC).

Intuition

GP is a grandparent of GC if GP is a parent of P and P is a parent of GC

Rules: Complex Predicates from Simple Queries

An Example: Defining a `grandparent` predicate

grandparent(GP, GC) :- parent(GP, P), parent(P, GC).

Querying The Defined Predicate

?- grandparent(X, kim). % who are the grandparents of kim
X = herbert ;           % hit ; to see next
X = felix   ;           % hit ; to see next
false.                  % thats it!

Rules: Complex Predicates from Simple Queries

An Example: Defining a `grandparent` predicate

grandparent(GP, GC) :- parent(GP, P), parent(P, GC).

Querying The Defined Predicate

?- grandparent(X, kim). % who are the grandparents of kim
X = herbert ;           % hit ; to see next
X = felix   ;           % hit ; to see next
false.                  % thats it!

How? Because Prolog can prove

?- parent(herbert, P), parent(P, kim).  %% Solution 1. X = herbert
P = margaret.

?- parent(felix, P), parent(P, kim).    %% Solution 2. X = felix
P = john .

QUIZ: Complex Predicates from Simple Queries

Which of the following is a valid greatgrandparent predicate?

(Btw, greatgrandparent is the parent of a grandparent.)

bob -> sachin -> krishna -> ranjit

% A
greatgrandparent(X, Y) :- parent(X, Y), grandparent(X, Y).

% B
greatgrandparent(X, Y) :- parent(X, Z), grandparent(Z, Y).

% C
greatgrandparent(X, Y) :- grandparent(X, Z), parent(Z, Y).

% D
greatgrandparent(X, Y) :- parent(X, Z), parent(Z, Y).

% E  
greatgrandparent(X, Y) :- parent(X, Z), parent(Z, Z1), parent(Z1, Y).

anc(albert,DESC) parent(albert, felix) ==> anc(felix, DESC) parent(albert, dana) ==> anc(dana, DESC)

anc(X, Y) :- anc(Z1, Y), parent(X, Z1).

anc(albert,DESC) anc(Z1, DESC) anc(Z1’, DESC) anc(Z1’‘, DESC) anc(Z1’’’, DESC)

Rules: Complex Predicates from Simple Queries

An Example: Defining a `greatgrandparent` predicate

greatgrandparent(GGP, GC) :- parent(GGP, GP), grandparent(GP, GC).

Rules: Complex Predicates from Simple Queries

An Example: Defining a `greatgrandparent` predicate

greatgrandparent(GGP, GC) :- parent(GGP, GP), grandparent(GP, GC).

Querying The Defined Predicate

?- greatgrandparent(X, holly).
X = herbert.

That was our first Prolog program!

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Prolog Programs = Facts + Rules!

Facts and Rules are two kinds of clauses

Fact: Clause without any conditions
Rules: Clause with conditions

Programs

Basic Facts / Predicates
Rules for generating new Facts / Predicates

Prolog Programs = Facts + Rules!

Complex Programs need Complex Predicates with Multiple Rules

Scope
Multiple Rules: Disjunction
Multiple Rules: Recursion

Prolog Programs = Facts + Rules!

Complex Programs need Complex Predicates with Multiple Rules

Scope
Multiple Rules: Disjunction
Multiple Rules: Recursion

Programs = Facts + Rules : Scope

A word about scope.

In the grandparent rule, the variable GP appears twice

greatgrandparent(GGP, GC) :- parent(GGP, GP), grandparent(GP, GC).

Scope: All Variables Are Local To A Single Rule

In Prolog, the scope of a variable is the single rule containing it.
There is no connection between variables across rules.

Programs = Facts + Rules : Scope

A word about scope.

Scope: All Variables Are Local To A Single Rule

In Prolog, the scope of a variable is the single rule containing it.
There is no connection between variables across rules.

Example

foo(P)   :- bar(P).     % There is no connection between P
stuff(P) :- thing(P).   % across the two rules

Prolog Programs = Facts + Rules!

Complex Programs need Complex Predicates with Multiple Rules

Scope
Multiple Rules: Disjunction
Multiple Rules: Recursion

Complex Predicates: Disjunction

Lets write a predicate has_family which is true for persons who

either have a parent
or have a child

Complex Predicates: Disjunction

Lets write a predicate has_family which is true for persons who

either have a parent
or have a child

has_family(X) :- parent(X, _). % if X is the parent of some _
has_family(X) :- parent(_, X). % if X is the child of some _

_ is a wildcard or dont-care variable (as in ML, Scala)

Disjunction via Multiple Rules

If we can prove parent(X, _) Then we can prove has_family(X)
If we can prove parent(_, X) Then we can prove has_family(X)

Complex Predicates: Disjunction

Lets write a predicate has_family which is true for persons who

either have a parent
or have a child

has_family(X) :- parent(X, _). % if X is the parent of some _
has_family(X) :- parent(_, X). % if X is the child of some _

Executing the Query

?- has_family(holly).
true.  % Second rule fires for holly

?- has_family(mugatu).
false. % Neither rule fires for mugatu

Complex Predicates: Disjunction

Lets write a predicate has_family which is true for persons who

either have a parent
or have a child

has_family(X) :- parent(X, _). % if X is the parent of some _
has_family(X) :- parent(_, X). % if X is the child of some _

Can be abbreviated to

has_family(X) :- parent(X, _) ; parent(_, X).

Semicolon ; indicates disjunction.

Prolog Programs = Facts + Rules!

Complex Programs need Complex Predicates with Multiple Rules

Scope
Multiple Rules: Disjunction
Multiple Rules: Recursion

Complex Predicates: Recursion

Lets write a predicate ancestor(Anc, Child) which is true if

parent(Anc, Child) … or
parent(Anc, P) and parent(P, Child) … or
parent(Anc, GP) and parent(GP, P) and parent(P, Child) … or
… if some chain of parent-links holds between Anc and Child.

Complex Predicates: Recursion

Lets write a predicate ancestor(Anc, Child) which is true if

… if some chain of parent-links holds between Anc and Child.

Base Case

If Anc is the parent of Child
ancestor(Anc, Child) :- parent(Anc, Child).

Inductive Case

If P is the parent of Child and Anc is an ancestor of P
ancestor(Anc, Child) :- parent(P, Child), ancestor(Anc, P).

Complex Predicates: Recursion

Lets write a predicate ancestor(Anc, Child) which is true if

… if some chain of parent-links holds between Anc and Child.

ancestor(Anc, Child) :- parent(Anc, Child).
ancestor(Anc, Child) :- parent(P, Child), ancestor(Anc, P).

Complex Predicates: Recursion

Lets write a predicate ancestor(Anc, Child) which is true if

… if some chain of parent-links holds between Anc and Child.

ancestor(Anc, Child) :- parent(Anc, Child).
ancestor(Anc, Child) :- parent(P, Child), ancestor(Anc, P).

Lets take it out for a spin!

First, lets find descendants (forwards)

?- ancestor(kim, X).
X = holly.

Complex Predicates: Recursion

Lets write a predicate ancestor(Anc, Child) which is true if

… if some chain of parent-links holds between Anc and Child.

ancestor(Anc, Child) :- parent(Anc, Child).
ancestor(Anc, Child) :- parent(P, Child), ancestor(Anc, P).

Lets take it out for a spin!

Next, lets find ancestors (backwards)

?- ancestor(X,kim).
X = margaret  ;
X = john      ;
X = herbert   ;
X = felix     ;
X = albert    .

kim has a long ancestry!

Pretty neat: go forward or back, in just 2 lines…

…Try doing that in any other language!

Plan

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking Search)

Backtracking Search

TBD

Order Matters!

TBD

Language

Terms
Facts
Queries (Implementation: Unification)
Rules
Programs (Implementation: Backtracking)

Programming

Numeric Computation
Data Structures
Puzzle Solving

Backtracking Search

How does prolog answer recursive queries?

Brute force backtracking search

View each clause as a proof rule:

goal :- subgoal_1, subgoal_2,...

Thus, the rules for ancestor are as follows:

ancestor(X,Y) :- parent(X,Y).			%rule 1
ancestor(X,Y) :- parent(Z,Y),ancestor(X,Z).	%rule 2

To prolog, these rules mean “to prove ancestor(X,Y), try to:

Prove the subgoal parent(X,Y), or, failing that,
Prove the subgoal parent(X,Z), **and then** the subgoalancestor(X,Z)`.

Suppose we ask it the query:

?- ancestor(felix,holly).

To prove this query, it undertakes the following backtracking search:

NOTE there are multiple Z variables (Z' and Z'' …)
These are introduced each time the corresponding sub-goals are triggered.

		ancestor(felix,holly)?
		  /		                \
  parent(felix,holly)    parent(Z,holly)
	  NO		               ancestor(felix,Z)
				|
				| Z = kim  (by fact)
				|
			  ancestor(felix,kim)
			  /                \
	  parent(felix,kim)     parent(Z',kim)
	      NO                ancestor(felix,Z')  ----------|
			                     |                            | Z'=john
		           Z'=margaret |                            |
				          |                             ancestor(felix,john)
		      ancestor(felix,margaret)                      |
		              /        \                      parent(felix,john)
	parent(felix,margaret)   parent(Z'',margaret)         YES
		          NO           ancestor(felix,Z'')
                                      |
		                    Z'' = herbert |
		                                  |
			                  ancestor(felix, herbert)
			                 /              |
		 parent(felix,herbert)   parent(Z''',herbert)
		            NO			             NO

Queries with Variables

Backtracking Search is done for every query.

  ?- ancestor(X,kim).

Prolog does the proof search
Returns all unifiers for X for which the proof succeeds with YES.

That is, literally programming by proving.

Hint: Trace mode in prolog shows the tree:

?- trace.
?- help(trace).

The subsequent query is traced…

Order is Very Important!

Order of clauses & terms influences unification & backtracking.

For each

goal different clauses are selected in order,
clause subgoals unified from left-to-right.

Bad Order Causes Non-Termination!

So, different orders of recursive sub-query can cause non-termination

Suppose we wrote:

ancestor(X,Y) :- ancestor(X,Z), parent(Z,Y).
ancestor(X,Y) :- parent(X,Y).

Then we see:

    ?- ancestor(felix,holly).

Why? The search tree looks like this now!

		ancestor(felix,holly)?
		  |
			|
			|
		ancestor(felix,Z)  %prove first subgoal,
			|          %then parent(Z,holly)
			|
			|
		ancestor(felix,Z') %prove first subgoal,
			|	   %then parent(Z',Z)
			|
			|
		ancestor(felix,Z'')
			.
			.
			.

To Avoid Stack Overflow

Place the parent subgoal first (in the recursive rule).
Then unification with the base facts (parent), fixes Z
Thereby guaranteeing termination.

QUIZ

Which of these will terminate?

% A
ancestor(X,Y) :- ancestor(X,Z), parent(Z,Y).
ancestor(X,Y) :- parent(X,Y).

% B
ancestor(X,Y) :- parent(X,Y).
ancestor(X,Y) :- ancestor(X,Z), parent(Z,Y).

% C
ancestor(X,Y) :- parent(X,Y).
ancestor(X,Y) :- parent(Z,Y), ancestor(X,Z).

% D
ancestor(X,Y) :- parent(Z,Y), ancestor(X,Z).
ancestor(X,Y) :- parent(X,Y).

QUIZ

Lets define a sibling predicate:

sibling(X, Y) if X and Y have the same parent.

% A
sibling(X, Y) :- parent(P, X), parent(P, Y).

% B
sibling(X, Y) :- parent(P, X), parent(P, Y), not(X = Y).

% C
sibling(X, Y) :- not(X = Y), parent(P, X), parent(P, Y).

Ordering and Unification

Unfortunately to prolog

?- X = Y.
X = Y

is always true, and so the not always fails

?- not(X = Y).
false.

So the following query always fails

if X and Y are variables!

sibling(X, Y) :- not(X = Y), parent(P, X), parent(P, Y).

Ensure Disequality Check After Unification

Solution

Ensure goal not(X=Y) fires after X and Y are unified to atoms

sibling(X, Y) :- parent(P, X), parent(P, Y), not(X = Y).

and now we get:

    ?- sibling(X,Y).
    X = john
    Y = maya ;

    X = felix
    Y = dana ;

    X = dana
    Y = felix ;

    X = maya
    Y = john ;
    No

Programming

Next, lets do some programmaing in prolog.

Numeric Computation
Data Structures
Puzzle Solving

Numeric Computation

Two big problems:

How do we even evaluate? e.g. 2 + 3 ?
How do we write functions e.g. let add x y = x + y ?

Problem 1: How to Evaluate?

Everything is a term and = is a unification operator:

?- X = 2 + 3.
X = 2 + 3

Pfft. To “compute” we need some evaluation mechanism!

Evaluation with the `is` Operator

The is operator lets us evaluate terms:

?- X is 2 + 3.
X = 5.

To solve is goal TERM1 is TERM2, prolog:

**Evaluates* TERM2 and then
Unifies result with TERM1.

However, watch out!

?- Y is X+2, X=1.
ERROR: Args are not sufficiently instantiated

?- X=1, Y is X+2.
X=1
Y=3

Variables must solved to numbers before evaluation.
Order of evaluation matters!

Numeric Computation

Two big problems:

How do we even evaluate? e.g. 2 + 1 ?
How do we write functions e.g. let incr x = x + 1 ?

Problem 2: How to Write Functions?

Oops. Everything is a predicate in prolog!

Facts are the basic predicates, and
Rules let us get new facts from the basic ones.

How can we even represent a function e.g.

let add x y = x + y

using predicates?

QUIZ

Which of the following represents let add x y = x + y?

% A
addP(X, Y) :- Z is X + Y.         % wtf is Z ?

% B
addP(X, Y, Z) :- Z is X + Y.      % wtf is Z ?

% C
addP(X, Y, X + Y).

% D
addP(X, Y) :- X + Y.

% E
addP(X, Y, Z) :- X + Y is Z.

Functions as Predicates

Every function of the form:

let foo x y = out

corresponds to a predicate of the form:

fooP(X, Y, OUT).

i.e. a predicate that is True for those triples (X, Y, OUT) s.t.

The function foo X Y evaluated to OUT!

The predicate captures the input-output relation of the function.

Factorial

Lets write a predicate capturing the IO relationship of factorial:

factorial(X, OUT)

holds only when OUT is the factorial of X.

**DO IN CLASS**

When we are done, we can call the function with a query:

	?- factorial(0, OUT).
	OUT = 1

	?- factorial(5, OUT).
	OUT = 120

Programming

Numeric Computation
Data Structures
Puzzle Solving

Data Structures: Lists

TBD

Programming

Numeric Computation
Data Structures
Puzzle Solving

Data Structures: Accumulators

TBD

Puzzle Solving

Towers of Hanoi
Farmer, Wolf, Goat, Cabbage

Towers of Hanoi

TBD

Farmer, Wolf, Goat, Cabbage

TBD